intervalles dans Z12
7×5/16e & 5×7/16e c.à.c 7 pour 5
9×7/16e & 7×9/16e 9 pour 7
6×11/16e & 5×13/16e 6 pour 5
14×5/16e & 10×7/16e 14 pour 10
& 7×5/8e & 5×7/8e 6teM-1/8e ton
10 pour 9 & 6×15/16e
11 pour 9
30
Les liens des métamorphoses
Modes de correspondances entre échelles
les liens des lieurs liants les re-liés
La théorie des ponts (encore une autre théorie * ! pour créer des liens)
Sans contact ni lien, une échelle n'a que l'utilité d'être un repère, une mesure, une approximation à l'accordage d'un instrument de musique. Comme les échelles nonoctaviantes Alpha, Beta et Gamma de Wendy Carlos qui divisent une 5te en 9, 11 et 20 notes ** et que l'on trouve dans « le bouquet » d'accordages proposé dans certains synthétiseurs VSTi (pourquoi ses 3 échelles furent élues et pas les autres ? est un mystère).
Pour former une théorie, il faut former des liens et des contacts entre les échelles et ce qu'elles engendrent : les modes et leurs dispositions : les gammes. Former un circuit qui donne des directions et des localisations pour identifier (caractériser) et créer des rapprochements puis des liaisons sensées (quoi que des liaisons insensées rentrent aussi dans le jeu de la musique et de l'humanité).
L'idée des ponts est de passer des gouffres (des espaces infranchissables) : le premier gouffre en musique (en vie humaine si tout est musique) se présente entre la conception quantitative (l'écriture) et la réalisation qualitative (la musique). Le passage ne va pas de soi, il n'y en a pas et pour qu'il se passe, il doit être éduqué : mémoriser les lois et les appliquer pour être conditionné, c'est-à-dire ne plus pouvoir percevoir autre chose au-delà de son conditionnement ou l'automation de son obéissance dans l'habitude ou autrement dit : sa culture. Nous et efforçons-nous à ce que les champs scalaires nonoctaviants n'obligent pas à une éducation.
INDICATION DES PASSAGES DE L'UNE A L'AUTRE
transitions (pas transposition) d'échelles
[début de mise en réseau du champ scalaire]
3 manières de passer :
A. par « saut » sans la nécessité d'un élément commun ou d'une connexion : par acrobatie.
B. par « glissade » sans la nécessité d'un élément commun ou d'une connexion : par mouvement global de l'échelle entière ou par mouvement local d'un seul degré.
C. par « équivalence linéaire » grâce à la conjonction d'un élément commun qui forme une connexion : un même dans des ensembles distincts.Le passage « linéaire » se réalise lorsqu'il y a connexion pour une correspondance,
c'est-à-dire un élément commun à deux ou plusieurs échelles : un unisson formé par 2 différences.
Un pont à un (ou plusieurs) degré commun entre différentes suites.
Les ponts, les tunnels sont des passages « linéaires »,
la téléportation est un passage par « saut »,
la déportation est un passage « en force »,
la mort est un passage par « glissade ».
PROCEDE DE DETECTION DES CONNEXIONS
PREMIERE
Correspondances sues
1. La première correspondance sue est réalisée par une origine commune entre échelles. C'est le rôle du diapason (fixe). Sans origine commune, les correspondances ne peuvent que se localiser en fréquences fixes mesurées en Hertz.
Les 2 origines usuelles commune 0 où une note correspond à une fréquence sont :
1. A3 (la3) <=> 440Hz (diapason)
ou/et
2. C3 (do3) <=> 261,62... Hz (note centrale du clavier piano) en fait pas tout à fait : le do3 médian porte le numéro 60, mi3 le n° 64 est la note du milieu des 128.2. La seconde correspondance sue est réalisée par les 2 bornes (hauteurs, notes, pitch, etc.) de l'ambitus divisé, l'intervalle qui sert de dividende.
3. La troisième correspondance sue est réalisée par la division paire de l'ambitus divisé. La division paire implique une moitié. Exemple : la 4te tempérée à 500 cents, sa moitié est 250 cents (2 tons et 1/4). La 5te tempérée à 700 cents, sa moitié est 350 cents (3 tons et 1/4). La 6te mineure tempérée à 800 cents, sa moitié est une 3ce majeure (400 cents). Pour la 7e mineuse tempérée à 1000 cents, sa moitié est une 4te. Etc.
La division paire de la moitié implique un quart. Tant que le nombre diviseur divisé est pair, la division paire se poursuit à 1/4, 1/8e, 1/16e, etc. Exemple : une division par 48 inclus une division par 24 inclut une division par 12 inclut une division par 6 inclus une division par 3. Une division par 38 n'implique qu'une moitié (un centre symétrique), car 19 sa moitié est impair et premier.4. La quatrième correspondance sue est réalisée quand une échelle est incluse totalement dans une autre. Exemple : l'échelle d'1/16e de ton inclut l'échelle d'1/8e de ton inclut l'échelle d'1/4 de ton inclut l'échelle d'1/2 ton inclut l'échelle par ton (gamme par ton découverte par Claude Debussy).
5. La cinquième correspondance sue est réalisée par la division paire différente du même ambitus et donne des bornes (hauteurs, notes, pitches, etc.) similaires. Exemple : la division paire de l'octave retrouve immanquablement la 4te+. La division paire de la 4te retrouve immanquablement l'intervalle 1 ton et 1/4 et sa borne correspondante. La division paire de la quinte retrouve immanquablement l'intervalle 1 ton et 1/2 et 1/4 (350 cents) avec sa borne correspondante.
Correspondances impossibles sues
1. La première correspondance impossible sue se réalise
Quand la division d'un intervalle inconnu et isolé est première.
Exemple : l'ambitus d'un instrument de musique normalisé est généralement ajusté en fonction de l'échelle tempérée Z12. Mais certains instruments de musique requièrent la possibilité de réaliser des ambitus sortant du tempérament Z12 : je pense aux cordes (V, Alt, Vcl, Cb), aux trombones, aux synthétiseurs analogiques où la fréquence des oscillateurs n'est pas crantée (scalairisée), aux synthétiseurs MIDI qui par ce protocole peuvent s'accorder sur n'importe quel ambitus, etc., pour les plus évidents.
...
2. La seconde correspondance impossible sue se réalise
Quand les différentes échelles n'ont pas une origine commune stable : note + fréquence connues.
...
SECONDE
Correspondances insues plutôt nonsues, même pas con sues mais : non sues
Détection des correspondances insues pas à l'insu des autres
A. correspondance numérique des intervalles | ou [parfois avec et] | B. correspondance sonore des intervalles à l'audition
Une correspondance numérique ne correspond pas obligatoirement à une correspondance audible
dans ce champ inconnu des échelles autre que Z12 tempérée et celles harmoniques (Zarlino, Werckmeister, Pythagore, Vallotti, Fokker, etc.) :
1. l'habitude millénaire de l'écoute scalaire de l'octave divisée en 12 parties + ou - égales conditionne à considérer d'autres échelles comme « fausses ».
2. le nombre est seul et unique, il n'a pas de contexte ni de conditionnement culturel dont nous avons besoin pour percevoir et échanger avec les autres ce qui est perçu par tous et ce que nous percevons nous-mêmes. Se conditionner c'est un peu comme accorder son instrument avec les autres, avec l'aide de la correspondance du diapason qui fait coïncider la même échelle Z12 pour tous. Dans le champ multiscalaire, la correspondance s'attache à faire communiquer différents degrés similarisés d'échelles différentes.Entre le chiffre et l'audition, il y a une pléthore d'intermédiaires.
...
DETECTION DES CONNEXIONS
I. Correspondance entre les échelles multiples (de 6) divisant le ton : les 8 1/ne de ton
8|1/ne de ton| = {1/16e de ton ; 1/15e de ton ; 1/14e de ton ; 1/13e de ton ; 1/12e de ton ; 1/11e de ton ; 1/10e de ton ; 1/9e de ton}
A. Correspondance interne des 11 premières échelles nonoctaviantes multiples d'1/16e de ton
dans Z96
[1/16e de ton <=> 12,5 cents]
Suite des correspondances intervallaires :
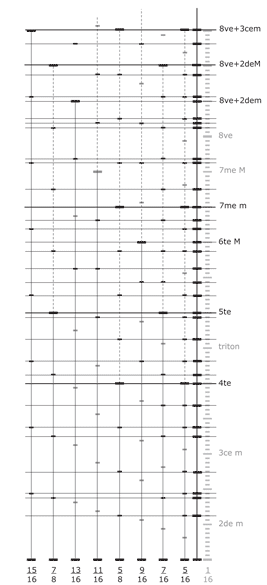
31 premières correspondances entre les 8 échelles nonoctaviantes de l'ensemble Z96 qui permettent la transition d'une échelle à une autre par au moins un élément commun.01. 2 . 5/16e & 1 . 5/8e
02. 2 . 7/16e & 1 . 7/8e
03. 3 . 5/16e & 1 . 15/16e
04.. 4 . 5/16e & 2 . 5/8e
05. 4 . 7/16e & 2 . 7/8e
06. 6 . 5/16e & 3 . 5/8e & 2 . 15/16e
07. 7 . 5/16e & 5 . 7/16e (2 échelles côte à côte dans un 7 pour 5)
08. 4te pour 8 . 5/16e & 4 . 5/8e
09. 6 . 7/16e & 3 . 7/8e
10. 9 . 5/16e & 5 . 9/16e & 3 . 15/16e
11. 10 . 5/16e & 5 . 5/8e
12. 11 . 5/16e & 5 . 11/16e (5te - 1/16e)
13. 5te pour 8 . 7/16e & 4 . 7/8e
14. 12 . 5/16e & 6 . 5/8e & 4 . 15/16e
15. 9 . 7/16e & 7 . 9/16e (2 échelles côte à côte dans un 9 pour 7)
16. 6 . 11/16e & 5 . 13/16e (2 échelles côte à côte dans un 6 pour 5)
17. 14 . 5/16e & 10 . 7/16e (2 échelles côte à côte dans un 14 pour 10) & 7 . 5/8e & 5 . 7/8e (6te M - 1/8e de ton)
18. 15 . 5/16e & 5 . 15/16e
19. 11 . 7/16e & 7 . 11/16e
20. 7em pour 16 . 5/16e & 8 . 5/8e
21. 12 . 7/16e & 6 . 7/8e
22. 18 . 5/16e & 10 . 9/16e & 9 . 5/8e (2 échelles côte à côte dans un 10 pour 9) & 6 . 15/16e
23. 13 . 7/16e & 7 . 13/16e
24. 14 . 7/16e & 7 . 7/8e
25. 11 . 9/16e & 9 . 11/16e
26. 20 . 5/16e & 10 . 5/8e
27. 21 . 5/16e & 15 . 7/16e (2 échelles côte à côte dans un 21 pour 15) & 7 . 15/16e
28. 22 . 5/16e & 11 . 5/8e & 9 . 11/16e (2 échelles côte à côte dans un 11 pour 9)
29. 8ve+2deM pour 16 . 7/16e & 8 . 7/8e
30. 13 . 9/16e & 9 . 13/16e
31. 8ve+3cem pour 24 . 5/16e & 12 . 5/8e & 8 . 15/16
...(lignes grisées horizontales dans le graphe)
La réunion des correspondances donne le mode suivant :
|
degré | x/16e de ton | cents | nom des intervalles dans Z12 |
points de correspondances | nombre de correspondances |
| 0 | 1 | 0 | origine | 1 | 8 | |
| 1 | 10/16e | 125 | 2×5/16e & 5/8e | 2 | ||
| 2 | 14/16e | 175 | 2×/16e & 7/8e | 2 | ||
| 3 | 15/16e | 187,5 | 3×5/16e & 15/16e | 2 | ||
| 4 | 20/16e | 250 | 4×5/16e & 2×5/8e | 2 | ||
| 5 | 28/16e | 350 | 4×7/16e & 2×7/8e | 2 | ||
| 6 | 30/16e | 375 | 6×5/16e & 3×5/8e & 2×15/16e | 3 | ||
| 7 | 35/16e | 437,5 | 7×5/16e & 5×7/16e c.à.c 7 pour 5 |
2 | ||
| 8 | 40/16e | 500 | 4te | 8×5/16e & 4×5/8e | 2 | |
| 9 | 42/16e | 525 | 6×7/16e & 3×7/8e | 2 | ||
| 10 | 45/16e | 562,5 | 9×5/16e & 5×9/16e & 3×15/16e | 3 | ||
| 11 | 50/16e | 625 | 10×5/16e & 5×5/8e | 2 | ||
| 12 | 55/16e | 687,5 | 11×5/16e & 5×11/16e 5te - 1/16e | 2 | ||
| 13 | 56/16e | 700 | 5te | 8×7/16e & 4×7/8e | 2 | |
| 14 | 60/16e | 750 | 12×5/16e & 6×5/8e & 4×15/16e | 3 | ||
| 15 | 63/16e | 787,5 | 9×7/16e & 7×9/16e 9 pour 7 |
2 | ||
| 16 | 66/16e | 825 | 6×11/16e & 5×13/16e 6 pour 5 |
2 | ||
| 17 | 70/16e | 875 | 14×5/16e & 10×7/16e 14 pour 10 |
4 | ||
| 18 | 75/16e | 937,5 | 15×5/16e & 5×15/16e | 2 | ||
| 19 | 77/16e | 962,5 | 11×7/16e & 7×11/16e | 2 | ||
| 20 | 80/16e | 1000 | 7e m | 16×5/16e & 8×5/8e | 2 | |
| 21 | 84/16e | 1050 | 12×7/16e & 6×7/8e | 2 | ||
| 22 | 90/16e | 1125 | 18×5/16e & 10×9/16e & 9×5/8e 10 pour 9 & 6×15/16e |
4 | ||
| 23 | 91/16e | 1137,5 | 13×7/16) & (7×13/16) | 2 | ||
| 24 | 98/16e | 1225 | 14×7/16e & 7×7/8e | 2 | ||
| 25 | 99/16e | 1237,5 | 11×9/16e &e 9×11/16e | 2 | ||
| 26 | 100/16e | 1250 | 20×5/16e & 10×5/8e | 2 | ||
| 27 | 105/16e | 1312,5 | 21×5/16e & 15×7/16e 21 pour 15 & 7×15/16e | 3 | ||
| 28 | 110/16e | 1375 | 22×5/16e & 11×5/8e & 9×11/16e 11 pour 9 |
3 | ||
| 29 | 112/16e | 1400 | 8ve+2deM | 16×7/16e & 8×7/8e | 2 | |
30 |
117/16e | 1462,5 | 13×9/16e & 9×13/16e | 2 | ||
| 31 | 120/16e | 1500 | 8ve+3cem | 24×5/16e & 12×5/8e & 8×15/16e | 3 | |
| etc. | etc. | etc. |
Ce mode des correspondances est une passerelle de passages composée des degrés communs des 8 premières échelles non-octaviantes de la famille d'1/16e de ton et où d'autres échelles étrangères (non multiples d'1/16e de ton) vont se connecter.Le mode des correspondances de connexions est comparable à la fonction de l'aéroport qui s'intègre dans un réseau plus vaste.
Nom : mode des correspondances d'1/16e de ton nonoctaviant p8. Ce mode des correspondances n'est pas cyclique. Ce mode ici couvre un ambitus de 1500 cents (8ve 3ce m) avec 31 degrés, mais n'est pas fini; il s'ajustera sans répétition selon l'instrument de musique utilisé pour sa fonction de reconnaissance des correspondances (sinon il servira à autre chose).
Téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler.** Notons que le script de Scala, en deça et au-delà des 31 degrés répète le mode à correspondances d'1/16e de ton nonoctaviant p8 comme un cycle à partir de l'origine do3 (261,63Hz) accordé au diapason la3 = 440 Hz.
Remarques :
. Tous les degrés des échelles de 5/8e, de 7/8e et de 15/16e de ton correspondent.
. 4 degrés de l'échelle de 7/16e de ton n'ont pas de correspondance contre 13 (hors origine) dans les premiers 31 degrés du mode.
. L'échelle de 9/16e de ton a 6 correspondances (hors origine) dans les premiers 31 degrés du mode contre 7 qui n'en n'ont pas.
. L'échelle de 11/16e de ton a 5 correspondances (hors origine) dans les premiers 31 degrés du mode contre 6 qui n'en n'ont pas.
. L'échelle de 13/16e de ton a 4 correspondances (hors origine) dans les premiers 31 degrés du mode contre 5 qui n'en n'ont pas.
. Dans ce contexte, il y a plus de hauteurs qui correspondent que de hauteurs isolées.
. Il serait intéressant de continuer la construction du « mode des correspondances 1/16e p8 » au-delà et en deçà pour comprendre sa forme...
. Les connexions semblent s'intensifier entre la 4te et la 7e mineure où il n'y a que 6 hauteurs isolées pour les 8 échelles.
. Cette famille est en attente de constitution modale combinée ou pas (avec plusieurs ou d'une seule échelle) et de vérification de ses transpositions exactes ou modifiées (où la taille change, mais pas les proportions), etc....
.
.
B. Correspondance interne des 9 premières échelles nonoctaviantes multiples d'1/15e de ton
dans Z90
[1/15e de ton <=> 13,33.. cents]
Suite des correspondances intervallaires :
30 premières correspondances entre les 7 échelles nonoctaviantes de l'ensemble Z90 qui permettent la transition d'une échelle à une autre par au moins un élément commun.
Nous nous sommes limités à deux cycles de 4/15e de ton.01. 2 . 4/15e & 1 . 8/15e
02. 3 . 4/15e & 1 . 4/5e
03. 2 . 7/15e & 1 . 14/15e
04. 4 . 4/15e & 2 . 8/15e
05. 6 . 4/15e & 3 . 8/15e & 2 . 4/5e
06. 7 . 4/15e & 4 . 7/15e & 2 . 14/15e
07. 8 . 4/15e & 4 . 8/15e
08. 9 . 4/15e & 3 . 4/5e
09. 10 . 4/15e & 5 . 8/15e
10. 6 . 7/15e & 3 . 14/15e
11. 11 . 4/15e & 4 . 11/15e
12. 12 . 4/15e & 6 . 8/15e & 4 . 4/5e
13. 13 . 4/15e & 4 . 13/15e
14. 14 . 4/15e & 8 . 7/15e & 7 . 8/15e & 4 . 14/15e
15. 15 . 4/15e & 5 . 4/5e = 6te mineure
16. 16 . 4/15e & 8 . 8/15e
17. 6 . 11/15e & 5 . 13/15e
18. 10 . 7/15e & 5 . 14/15e
19. 18 . 4/15e & 9 . 8/15e & 6 . 4/5e
20. 11 . 7/15e & 7 . 11/15e
21. 20 . 4/15e & 10 . 8/15e
22. 21 . 4/15e & 12 . 7/15e & 7 . 4/5e & 6 . 14/15e
23. 22 . 4/15e & 11 . 8/15e & 8 . 11/15e
24. 13 . 7/15e & 7 . 13/15e
25. 24 . 4/15e & 12 . 8/15e & 8 . 4/5e
26. 14 . 7/15e & 7 . 14/15e
27. 26 . 4/15e & 13 . 8/15e & 8 . 13/15e
28. 27 . 4/15e & 9 . 4/5e
29. 28 . 4/15e & 16 . 7/15e & 14 . 8/15e & 8 . 14/15e
30. 30 . 4/15e & 15 . 8/15e & 10 . 4/5e = 8ve + 3ce majeure
...(lignes grisées horizontales dans le graphe)
La réunion des correspondances donne le mode suivant :
Des premiers 30 degrés, l'échelle de 4/15e de ton rassemble presque toutes les correspondances sauf le 3eme, le 10eme, le 17eme, le 18eme, le 20eme, le 24eme et le 26eme : 7 degrés sur 23.
degré x/15e de ton cents nom des
intervalles dans Z12points de correspondances nombre de correspondances 0 1 0 origine 1 7 1 8/15e 106,667 2×4/15e & 8/15e 2 2 4/5e 160 3×4/15e & 4/5e 2 3 14/15e 186,667 2×7/15e & 14/15e 2 4 16/15e 213,334 4×4/15e & 2×8/15e 2 5 8/5e 320 6×4/15e & 3×8/15e & 2×4/5e 3 6 28/15e 373,334 7×4/15e & 4×7/15e & 2×14/15e 3 7 32/15e 426,667 8×4/15e & 4×8/15e 2 8 12/5e 480 9×4/15e & 3×4/5e 2 9 8/3e 533,334 10×4/15e & 5×8/15e 2 10 14/5e 560 6×7/15e & 3×14/15e 2 11 44/15e 586,667 11×4/15e & 4×11/15e 2 12 48/15e 640 12×4/15e & 6×8/15e & 4×4/5e 3 13 52/15e 693,334 13×4/15e & 4×13/15e 2 14 56/15e 746,667 14×4/15e & 8×7/15e & 7×8/15e & 4×14/15e 4 15 12/3 800 6te m 15×4/15e & 5×4/5e 2 16 64/15e 853,334 16×4/15e & 8×8/15e 2 17 22/5e 880 6×11/15e & 5×13/15e 2 18 14/3 933,334 10×7/15e & 5×14/15e 2 19 24/5e 960 18×4/15e & 9×8/15e & 6×4/5e 3 20 77/15e 1026,667 11×7/15e & 7×11/15e 2 21 16/3 1066,667 20×4/15e & 10×8/15e 2 22 28/5e 1120 21×4/15e & 12×7/15e & 7×4/5e & 6×14/15e 4 23 88/15e 1173,334 22×4/15e & 11×8/15e & 8×11/15e 3 24 91/15e 1213,334 13×7/15e & 7×13/15e 2 25 32/5e 1280 24×4/15e & 12×8/15e & 8×4/5e 3 26 98/15e 1306,667 14×7/15e & 7×14/15e 2 27 104/15e 1386,667 26×4/15e & 13×8/15e & 8×13/15e 3 28 108/15e 1440 27×4/15e & 9×4/5e 2 29 112/15e 1493,334 28×4/15e & 16×7/15e & 14×8/15e & 8×14/15e 4 30 24/3 1600 8ve + 3ce M 30×4/15e & 15×8/15e & 10×4/5e 3 etc. etc. etc. Dans sa forme nous constatons dans ce mode des correspondances, des rapports de phases d'échelles où le mode des correspondances résultant ne se répète jamais : n'est pas cyclique; cela par les "glissement" constants de ses 7 cycles les uns sur les autres. Ce sont les mêmes principes que les déphasages rythmiques initiés par Steve Reich avec Drumming ou Piano Phase par exemple, mais ici dans le champ des hauteurs. Ce mode ici couvre un ambitus de 1600 cents avec 30 degrés, mais n'est pas fini; il s'ajustera sans répétition selon l'instrument de musique utilisé pour sa fonction de reconnaissance des correspondances (sinon il servira à autre chose).
Téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler.Ce mode des correspondances est une passerelle de passage où toutes les 7 premières échelles non-octaviantes de cette famille où d'autres peuvent se connecter : comparable à la fonction de l'aéroport qui s'intègre dans un réseau plus vaste. Nom : mode des correspondances d'1/15e de ton non-octaviant p7. Ce mode des correspondances n'est pas cyclique*.
* Notons que le script de Scala, en deça et au-delà des 30 degrés répète le mode à correspondances d'1/15e de ton non-octaviant p7 comme un cycle à partir à partir de l'origine do3 (261,63Hz) accordé au diapason du la3 (A4) = 440 Hz.
...
.
.
C. Correspondance interne des 6 premières échelles nonoctaviantes multiples d'1/14e de ton
dans Z84
[1/14e de ton <=> 14,28... cents]
Suite des correspondances intervallaires :
22 premières correspondances entre les 6 échelles nonoctaviantes de l'ensemble Z84 qui permettent la transition d'une échelle à une autre par au moins un élément commun.01. 2 . 5/14e & 1 . 5/7e
02. 4 . 5/14e & 2 . 5/7e
03. 6 . 5/14e & 3 . 5/7e
04. 8 . 5/14e & 4 . 5/7e
05. 9 . 5/14e & 5 . 9/14e
06. 10 . 5/14e & 5 . 5/7e
07. 11 . 5/14e & 5 . 11/14e
08. 12 . 5/14e & 6 . 5/7e
09. 6 . 11/14e & 5 . 13/14e
10. 14 . 5/14e & 7 . 11/14e = 7e mineure
11. 9 . 4/7e & 8 . 9/14e
12. 16 . 5/14e & 10 . 4/7e & 8 . 5/7e
13. 11 . 4/7e & 8 . 11/14e
14. 18 . 5/14e & 10 . 9/14e & 9 . 5/7e
15. 11 . 9/14e & 9 . 11/14e
16. 20 . 5/14e & 10 . 5/7e
17. 13 . 4/7e & 8 . 13/14e
18. 22 . 5/14e & 11 . 5/7e & 10 . 11/14e
19. 13 . 9/14e & 9 . 13/14e
20. 24 . 5/14e & 15 . 4/7e & 12 . 5/7e
21. 26 . 5/14e & 13 . 5/7e & 10 . 13/14e
22. 27 . 5/14e & 15 . 9/14e
...(lignes grisées horizontales dans le graphe)
La réunion des correspondances donne le mode suivant :
degré x/14e de ton cents nom des
intervalles dans Z12points de correspondances nombre de correspondances 0 1 0 origine 1 6 1 5/7e 142,857... 2×5/14e & 1×5/7e 2 2 10/7e 285,714... 4×5/14e & 2×5/7e 2 3 15/7e 428,571... 6×5/14e & 3×5/7e 2 4 20/7e 571,428... 8×5/14e & 4×5/7e 2 5 45/14e 642,857... 9×5/14e & 5×9/14e 2 6 25/7e 714,285... 10×5/14e & 5×5/7e 2 7 55/14e 785,714... 11×5/14e & 5×11/14e 2 8 30/7e 857,142... 12×5/14e & 6×5/7e 2 9 33/7e 942,857... 6×11/14e & 5×13/14e 2 10 35/7e 1000 7e mineure 14×5/14e & 7×11/14e 2 11 36/7e 1028,571... 9×4/7e & 8×9/14e 2 12 40/7e 1142,857... 16×5/14e & 10×4/7e & 8×5/7e 3 13 44/7e 1257,142... 11 . 4/7e & 8 . 11/14e 2 14 45/7e 1285,714... 18×5/14e & 10×9/14e & 9×5/7e 3 15 99/14e 1414,2857... 11×9/14e & 9×11/14e 2 16 50/7e 1428,571... 20×5/14e & 10×5/7e 2 17 52/7e 1485,714... 13×4/7e & 8×13/14e 2 18 55/7e 1571,428... 22×5/14e & 11×5/7e & 10×11/14e 3 19 117/14e 1671,428... 13×9/14e & 9×13/14e 2 20 60/7e 1714,285... 24×5/14e & 15×4/7e & 12×5/7e 3 21 65/7e 1857,142... 26×5/14e & 13×5/7e & 10×13/14e 3 22 135/14e 1928,571... 27×5/14e & 15×9/14e 2 remarques :
. Tous les degré de l'échelle de 5/7e de ton correspondent, principalement avec sa moitié : l'échelle de 5/14e de ton
. L'échelle de 4/7e de ton a 6 correspondances (hors origine) dans les premiers 22 degrés
. L'échelle de 9/14e de ton a 6 correspondances (hors origine) dans les premiers 22 degrés
. L'échelle de 11/14e de ton a 5 correspondances (hors origine) dans les premiers 22 degrés
. L'échelle de 13/14e de ton a 4 correspondances (hors origine) dans les premiers 22 degrésCe mode ici couvre un ambitus de 1928,571... cents avec 22 degrés, mais n'est pas fini; il s'ajustera sans répétition selon l'instrument de musique utilisé pour sa fonction de reconnaissance des correspondances (sinon il servira à autre chose).
Téléchargez le Scala tuning script .scl, download the tuning script for Kontakt sampler.*Ce mode des correspondances est une passerelle de passage où toutes les 6 premières échelles nonoctaviantes de cette famille où d'autres peuvent se connecter :
comparable à la fonction de l'aéroport qui s'intègre dans un réseau plus vaste.
Nom : mode des correspondances d'1/14e de ton nonoctaviant p6. Ce mode des correspondances n'est pas cyclique*.* Notons que le script de Scala, en deça et au-delà des 22 degrés répète le mode à correspondances d'1/14e de ton non-octaviant p6 comme un cycle à partir à partir de l'origine do3 (261,63Hz).
...
.
.
D. Correspondance interne des 8 premières échelles nonoctaviantes multiples d'1/13e de ton
dans Z78
[1/13e de ton <=> 15,38... cents]
Suite des correspondances intervallaires :
46 premières correspondances entre les 8 échelles nonoctaviantes de l'ensemble Z78 qui permettent la transition d'une échelle à une autre par au moins un élément commun.01.
...(lignes grisées horizontales dans le graphe)
La réunion des correspondances donne le mode suivant :
Mode des correspondances pour les 8 premières échelles nonoctaviantes multiples de Z78 (1/13e de ton) :
degré x/13e de ton cents nom des
intervalles dans Z12points de correspondances nombres de correspondances 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 24/13e 6×4/13e & 3×8/13e & 2×12/13e 3 5 20/13e 5×4/13e & 4×5/13e 5pour4 & 2×10/13e 3 4 16/13e 4×4/13e & 2×8/13e & 16/13e 3 3 12/13e 3×4/13e & 12/13e 2 2 10/13e 2×5/13e & 10/13e 2 1 8/13e 123,077 2×4/13e & 8/13e 2 0 1 0 origine 1 8 ...
E. Correspondance interne des 8 premières échelles nonoctaviantes multiples d'1/12e de ton
dans Z72
[1/12e de ton <=> 16,66.. cents]
F. Correspondance interne des 8 premières échelles nonoctaviantes multiples d'1/11e de ton
dans Z66
[1/11e de ton <=> 18,18.. cents]
G. Correspondance interne des 8 premières échelles nonoctaviantes multiples d'1/10e de ton
dans Z60
[1/10e de ton <=> 20 cents]
H. Correspondance interne des 8 premières échelles nonoctaviantes multiples d'1/9e de ton
dans Z54
[1/9e de ton <=> 22,22.. cents]
.
.
.
A inter B inter C inter D inter E inter F inter G inter H
∩
PASSAGES - TRANSFORMATIONS - MUTATIONS - TRANSITIONS
= le sens des CHAMPS SCALAIRES : les liens
1er essai de liaison (de mise ensemble) des 4 modes de correspondances issus des nonoctaviantes 1/16e, 1/15e, 1/14e et 1/13e de ton (manque 1/12e, 1/11e, 1/10e, 1/9e)
Nous allons maintenant former un tableau graphique avec toutes les 53 échelles nonoctaviantes, afin de réaliser les passages des unes aux autres : seules, ces échelles n'ont que l'intérêt de proposer d'autres accordages. Ensembles, elles forment un Champ Scalaire d'opérations possibles. Ce que nous allons construire, est la possibilité de transformations (métaboles) entres elles, formant la toile élastique pour la formation des modes et des accords (chords) propre à leurs sonorités suivant leurs positions dans la toile à tel moment. Ce n'est que l'amorce d'un début... des Champs Scalaires pour le voyage (interplanétaire : à chaque planète son horloge) et la formation de modes avec leurs gammes originales et uniques.
[premier schéma du Champ Scalaire en cours]
C'est à ce stade que nous allons connaître l'utilité des modes des correspondances des 8 groupes d'échelles nonoctaviantes : au lieu de mettre en correspondance 53 échelles telles quelles, nous allons mettre en correspondance les 8 modes des correspondances de chaque groupe d'échelles nonoctaviantes appartenant aux 8 groupes 1/16e, 1/15e, 1/14e, 1/13e, 1/12e, 1/11e, 1/10e et 1/9e de ton tel que :
mode des correspondances d'1/16e de ton nonoctaviant p8 avec mode des correspondances d'1/15e de ton nonoctaviant p7 avec mode des correspondances d'1/14e de ton nonoctaviant p6 avec mode des correspondances d'1/13e de ton nonoctaviant p8 avec mode des correspondances d'1/12e de ton nonoctaviant p4 avec mode des correspondances d'1/11e de ton nonoctaviant p6 avec mode des correspondances d'1/10e de ton nonoctaviant p3 avec mode des correspondances d'1/9e de ton nonoctaviant p4 :
Correspondances entre les modes de correspondances nonoctaviants
{ (96√2)6 ∩ (96√2)7 ∩ (96√2)9 ∩ (96√2)10 ∩ (96√2)11 ∩ (96√2)13 ∩ (96√2)14 ∩ (96√2)15 } ∩ { (90√2)4 ∩ (90√2)7 ∩ (90√2)8 ∩ (90√2)11 ∩ (90√2)12 ∩ (90√2)13 ∩ (90√2)14 } ∩ { (84√2)5 ∩ (84√2)8 ∩ (84√2)9 ∩ (84√2)10 ∩ (84√2)11 ∩ (84√2)13 } ∩ { (78√2)4 ∩ (78√2)5 ∩ (78√2)7 ∩ (78√2)8 ∩ (78√2)9 ∩ (78√2)10 ∩ (78√2)11 ∩ (78√2)12 } ∩ { (72√2)5 ∩ (72√2)7 ∩ (72√2)10 ∩ (72√2)11 } ∩ { (66√2)4 ∩ (66√2)5 ∩ (66√2)7 ∩ (66√2)8 ∩ (66√2)9 ∩ (66√2)10 } ∩ { (60√2)7 ∩ (60√2)8 ∩ (60√2)9 } ∩ { (56√2)4 ∩ (56√2)5 ∩ (56√2)7 ∩ (56√2)8 }
1. positionnement :
8 nonoctaves de Z96 (96√2=1,00725) contre 8 échelles octaviantes
5 (96√2)6 = 1,03678
7 (96√2)7 = 1,05187
9 (96√2)9 = 1,06717
10 (96√2)10 = 1,07491
11 (96√2)11 = 1,0827
13 (96√2)13 = 1,09846
14 (96√2)14 = 1,10642
15 (96√2)15 = 1,11445Mode de correspondance d'1/16e de ton nonoctaviant p8 de Z96 { (96√2)6 ∩ (96√2)7 ∩ (96√2)9 ∩ (96√2)10 ∩ (96√2)11 ∩ (96√2)13 ∩ (96√2)14 ∩ (96√2)15 }
7 nonoctaves de Z90 (90√2=1,00773) contre 8 échelles octaviantes
4 (90√2)4 = 1,03128...
7 (90√2)7 = 1,05538...
8 (90√2)8 = 1,06354...
11 (90√2)11 = 1,08839...
12 (90√2)12 = 1,09681...
13 (90√2)13 = 1,10529...
14 (90√2)14 = 1,11383...16 (90√2)16 = 1,13114...
17 (90√2)17 = 1,13988...Mode de correspondance d'1/15e de ton nonoctaviant p7 de Z90 { (90√2)4 ∩ (90√2)7 ∩ (90√2)8 ∩ (90√2)11 ∩ (90√2)12 ∩ (90√2)13 ∩ (90√2)14 }
6 nonoctaves de Z84 (84√2=1,00829) contre 8 échelles octaviantes
5 (84√2)5 = 1,04214...
8 (84√2)8 = 1,06828
9 (84√2)9 = 1,07713
10 (84√2)10 = 1,08606
11 (84√2)11 = 1,09507
13 (84√2)13 = 1,1133Mode de correspondance d'1/14e de ton nonoctaviant p6 de Z90 { (84√2)5 ∩ (84√2)8 ∩ (84√2)9 ∩ (84√2)10 ∩ (84√2)11 ∩ (84√2)13 }
8 nonoctaves de Z78 (78√2=1,00892) contre 5 échelles octaviantes
4 (78√2)4 = 1,03618...
5 (78√2)5 = 1,04543...
7 (78√2)7 = 1,06418...
8 (78√2)8 = 1,07368...
9 (78√2)9 = 1,08326...
10 (78√2)10 = 1,09293...
11 (78√2)11 = 1,10268...
12 (78√2)12 = 1,11253...Mode de correspondance d'1/13e de ton nonoctaviant p8 de Z78 { (78√2)4 ∩ (78√2)5 ∩ (78√2)7 ∩ (78√2)8 ∩ (78√2)9 ∩ (78√2)10 ∩ (78√2)11 ∩ (78√2)12 }
4 nonoctaves de Z72 (72√2=1,00967) contre 8 échelles octaviantes
5 (72√2)5 = 1,04929...
7 (72√2)7 = 1,06969...
10 (72√2)10 = 1,10102...
11 (72√2)11 = 1,11167...Mode de correspondance d'1/12e de ton nonoctaviant p4 de Z72 { (72√2)5 ∩ (72√2)7 ∩ (72√2)10 ∩ (72√2)11 }
6 nonoctaves de Z66 (66√2=1,00967) contre 5 échelles octaviantes
4 (66√2)4 = 1,03924...
5 (66√2)5 = 1,04929...
7 (66√2)7 = 1,06969...
8 (66√2)8 = 1,08003...
9 (66√2)9 = 1,09047...
10 (66√2)10 = 1,1224...Mode de correspondance d'1/11e de ton nonoctaviant p6 de Z66 { (66√2)4 ∩ (66√2)5 ∩ (66√2)7 ∩ (66√2)8 ∩ (66√2)9 ∩ (66√2)10 }
3 nonoctaves de Z60 (60√2=1,01055) contre 7 échelles octaviantes
7 (60√2)7 = 1,06969...
8 (60√2)8 = 1,08003...
9 (60√2)9 = 1,09047...Mode de correspondance d'1/10e de ton nonoctaviant p3 de Z60 { (60√2)7 ∩ (60√2)8 ∩ (60√2)9 }
4 nonoctaves de Z54 (54√2=1,01292) contre 5 échelles octaviantes
4 (56√2)4 = 1,05269
5 (56√2)5 = 1,06629
7 (56√2)7 = 1,09402
8 (56√2)8 = 1,10816Mode de correspondance d'1/9e de ton nonoctaviant p4 de Z56 { (56√2)4 ∩ (56√2)5 ∩ (56√2)7 ∩ (56√2)8 }
.
...
Notes
* Députation d'une cité pour un évènement politique ou religieux. Députation ne signifie pas retirer les putes de la cité, mais de disposer les députés à missionner autrement dit à créer des liens officiels dont les populations doivent être témoins (pas de politique ni de religion sans un « peuple » et son témoignage public) c'est en ça que politiciens et religieux sont des parasites : sans peuple croyant, ils disparaissent. Les théories se suivent et se « raessemblent » dans le ralliement, comme la formation du réseau de communication. Un ensemble d'idées reliées pour faire fonctionner un état d'esprit, une habitude ou une machine.
** Alpha dispose 15,4285... notes par octave, Beta dispose 18,857... notes par octave et attire une octaviation au 19e degré à 9 cents près, Gamma dispose 34,2857... notes par octave. Si Wendy a proposé une théorie à partir de ses 3 échelles, elle ne l'a pas communiqué.
re tour à la table des matières
