Comprendre TOD : le traitement occidental des durées en musique

où l'assemblage de durées ne fait pas le rythme

TOD a dit

 

L'évaluation du temps des Blancs se repose sur la rotation de notre planète sur elle-même (jour/nuit). La seconde, • = 60bpm (battements par minute) est définie comme une fraction du jour de la Terre éclairée par le Soleil. La seconde est l'unité de base du temps « de la science » des Blancs. Les Blancs ont 2 manières de mesurer le temps : 1. de la division du mouvement continu qui donne une échelle de temps chronologique et 2. du cumul d'une durée de temps, un temps étalon qui donne une fréquence étalon pour mesurer les durées indépendamment de la date. Par exemple, la perception des changements et la mémoire que nous en avons illustre l'échelle de chronologie. Elle est une référence qui permet de « classer » (oui, les Blancs aiment ordonner les choses et les êtres) les évènements (successifs ou bien et simultanés) en leur donnant des dates (les Blancs apprécient avoir une mémoire éternelle). L’idée de durée de temps a éclot grâce à la croyance des Blancs qu'il existe des intervalles de temps égaux qui permettent à une même action de se répéter (la mécanisation). La durée est définie par le temps de l'écoulement du sable dans le sablier. Les horaires forment (entre autres) une échelle chronologique; découpés en secondes, minutes, heures, jours, mois, années, siècles, etc. Dans la pratique, les échelles de temps ne sont pas parfaitement uniformes malgré la tendance volontaire à vouloir un temps universel TU, un temps terrestre commun pour tous (dont l'origine est à l'observatoire de Greenwich en Angleterre). D'autres temps existent, comme le temps des éphémérides TE (pour les mesures astronomiques non terrestres) qui se base sur la révolution de la Terre autour du Soleil (saisons) ou le temps atomique TA (devenu la base de la définition de la seconde) basé sur les vibrations internes des atomes (TA qui forme des horloges atomiques plus précises et plus stables que nos horloges à quartz qui équipent nos montres d'aujourd'hui). Mais pour toutes les horloges, aussi précise soit-elle, la relation t'B - t'A = tB - tA ne se vérifie pas dans le « flux temporel », mais s'applique dans les machines. Une échelle chronologique n'a pas de durée, bien qu'on puisse en déduire une; d'une date à une autre (considéré comme quantité qui est source de confusion). Dans la musique occidentale, cette distinction existe aussi : où l'une est nommée suite arithmétique (succession de durées) et l'autre suite géométrique (division du continuum). Les Blancs ont assimilé la succession des durées au chant sans battue alors que la division du continuum temporel est assimilée à la danse avec battue chronologique généralement commune (le même tempo pour tous qui est fixé suivant la danse).

Une horloge définit une échelle de temps. Chacun suivant sa constitution, dispose de sa propre horloge biologique (aux longueurs d'onde et fréquences variables) qui rythme ses actes dans la durée de sa vie. Les ordinateurs par exemple ont une horloge qui n'a pas la même forme que celle des humains : elle est mécanique et accordée sur l'échelle du TU. Les pierres n'ont pas la même horloge que les arbres ou l'herbe et ont des durées de vie différentes : les insectes, les bactéries, les atomes, les quarks, les cellules, les méduses, les baleines, etc., où nous sommes tous, êtres vivants des horloges. Il y a autant de choses et d'êtres qu'il y a d'échelles de temps, malgré que chaque Blanc soit éduqué à être à la même heure au même moment, qu'il court après le temps, n'a pas le temps et s'en plaint constamment.

...

 

pour approfondir
. La mesure du temps (Bernard Decaux & Bernard Guinot, Que sais-je 1969)
. Le Papalagui, paroles de Touiavii chef de la tribu de Tiavéa des îles Samoa (recueillies par Erich Scheurmann, 1914-1930. Traduction française ~ 1983)
. La naissance de la tragédie (Friedrich Nietzsche, 1872)
. L'intuition de l'instant (Gaston Bachelard, 1932)

 

 

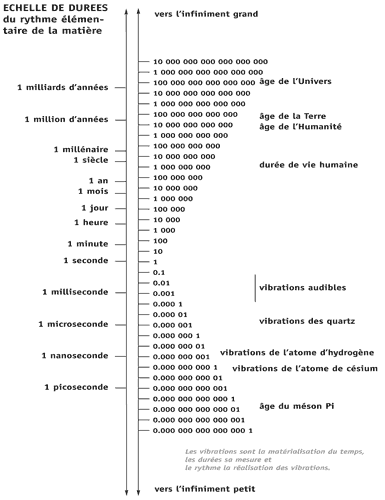
[graphe de l'échelle de durées multiple de 10 :
de l'âge du méson pi à celuis de l'univers,
incluant l'intervalle des vibrations humainement audibles]

cuisine de compositeur :

 

Nous allons tenter de rapprocher : durée et intervalle de temps.
Et découvrir les caractéristiques des suites de durées et d'intervalles.

 

1.

Basiquement (au fur et à mesure depuis le XIVe siècle), nous utilisons des valeurs de durée simples de rapport 2 (avant Ars Nova, la musique était principalement ternaire) : doubler ou jouer la moitié (multiplier ou diviser par 2) moins par 3 d'où la notation suivante :

Suite de durées de rapport 2 (binaire) :

symbole nom rapport valeurs numériques
durées de temps intervalles de temps
•|||| quadruple croche   1 1/128
•||| triple croche 2 2 1/64
•|| double croche 2 4 1/32
•| croche 2 8 1/16
• noire 2 16 1/8
o blanche 2 32 1/4
O ronde 2 64 1/2
□ carrée 2 128 1

avec origine : 1 noté •||||, constante (raison) : 2, opération ×, unité ppcm : 1 (plus petit commun multiple)
avec origine : 128 noté □, constante (raison) 2, opération ÷, unité pgcd : 1 (plus grand commun diviseur)

Dans cette suite de constante (ou de raison) 2, durées de temps concordent avec intervalles de temps. Cette concordance permet un passage sans heurt d'un chant sans battue à une danse bien battue. Mais cette suite ne possède que 8 durées qui réduisent la subtilité de la musique.

remarque : le rapport 2 dans le champ des hauteurs correspond à l'intervalle de l'octave (8ve).

représentation proportionnelle de la suite binaire des 8 valeurs de durées

 

INTRODUCTION DU POINT :
une valeur pointée est une valeur allongée de la moitié de sa valeur :
le point a aussi une fonction binaire (÷2), mais donne un résultat ternaire et binaire et premier.
[exemple : 2pointé = 3 (3 est ternaire); 5pointé = 7,5 (7,5 est premier); 4pointé = 6 (6 est binaire et ternaire)]

Le pointage de la note de musique sert à passer du ternaire au binaire et vice versa sans changer de mesure.

2.

L'ajout du point à ces 8 valeurs de durée nous donne une suite à deux rapports alternés : 3/2 et 4/3.

Suite de durées de rapports 3/2 et 4/3 :
symbole nom rapports valeurs numériques
durées de temps intervalles de temps
•||| triple croche   2 1/96 1/64
•|||. triple croche pointée 3/2 3 1/64 3/128
•|| double croche 4/3 4 1/48 1/32
•||. double croche pointée 3/2 6 1/32 3/64
•| croche 4/3 8 1/24 1/16
•|. croche pointée 3/2 12 1/16 3/32
• noire 4/3 16 1/12 1/8
•. noire pointée 3/2 24 1/8 3/16
o blanche 4/3 32 1/6 1/4
o. blanche pointée 3/2 48 1/4 3/8
O ronde 4/3 64 1/3 1/2
O. ronde pointée 3/2 96 1/2 3/4
□ carrée 4/3 128 2/3 1
□. carrée pointée 3/2 192 1  

avec
origine : 2 noté •|||, constantes (de raison) 3/2 puis 4/3, opération : ×, unité : 1

Dans cette suite de 14 valeurs de constantes (ou de raison) 3/2 puis 4/3, durées de temps concordent avec intervalles de temps. Cette concordance permet un passage sans heurt d'un chant sans battue à une danse bien battue. Les 7 valeurs pointées seules ont un rapport de 2. Les 7 valeurs non pointées seules ont un rapport de 2. L'ajout de 7 valeurs pointées augmente la suite des durées à 15 durées. Une durée pointées est à la fois une valeur binaire et une valeur ternaire.

remarques :
Les rapports 3/2 et 4/3 dans le champ des hauteurs sont nommés : quinte (5te) et quarte (4te).
Le tempo du rythme correspond au diapason des hauteurs : il donne la vitesse sur laquelle tout le monde s'accorde.

plus loin :

3.

L'ajout du double point nous donne une suite de valeurs qui divisent le rapport 2 en 3/2 × 7/6 × 8/7 (où 4/3 = 7/6 × 8/7)

Suite de durées de rapports 3/2, 7/6 et 8/7
symbole nom rapports valeurs numériques
durées de temps intervalles de temps
•|| double croche 3/2 4 1/48 1/32
•||. double croche pointée 7/6 6 3/112 3/64
•||.. double croche doublement pointée 8/7 7 1/32 7/128
•| croche 3/2 8 1/24 1/16
•|. croche pointée 7/6 12 3/56 3/32
•|.. croche doublement pointée 8/7 14 1/16 7/64
• noire 3/2 16 1/12 1/8
•. noire pointée 7/6 24 3/28 3/16
•.. noire doublement pointée 8/7 28 1/8 7/32
o blanche 3/2 32 1/6 1/4
o. blanche pointée 7/6 48 3/14 3/8
o.. blanche doublement pointée 8/7 56 1/4 7/16
O ronde 3/2 64 1/3 1/2
O. ronde pointée 7/6 96 3/7 3/4
O.. ronde doublement pointée 8/7 112 1/2 7/8
□ carrée 3/2 128 4/7 1
□. carrée pointée 7/6 192 6/7  
□.. carrée doublement pointée 8/7 224 1  

avec
origine : 4 noté •||, constantes (de raison) 3/2 puis 7/6 puis 8/7, opération : ×, unité : 1

Dans cette suite de 18 valeurs, durées de temps concordent avec intervalles de temps. Cette concordance permet un passage sans heurt d'un chant sans battue à une danse bien battue. L'ajout de 6 valeurs doublement-pointées augmente la suite des durées à 21 durées. Les 6 valeurs doublement pointées seules ont un rapport de 2. Les 6 valeurs pointées seules ont un rapport de 2. Les 6 valeurs non pointées seules ont un rapport de 2. Une durée doublement pointées est une valeur binaire (qui ne se divise pas par 3).

remarque :
Les rapports 7/6 et 8/7 dans le champ des hauteurs harmoniques sont nommés : tierce mineure (3ce m) septimal (contre 6/5 tierce mineure et 5/4 tierce majeure) et ton (2de M) septimal.

plus loin :

4.

L'ajout du triple point nous donne une suite de valeurs qui divisent le rapport 2 en 3/2 × 7/6 × 15/14 × 16/15 (où 8/7 = 15/14 × 16/15)

Suite de durées de rapports 3/2, 7/6, 15/14 et 16/15
symbole nom rapports valeurs numériques
durées de temps intervalles de temps
•| croche 3/2 8 1/24 1/16
•|. croche pointée 7/6 12 3/56 3/32
•|.. croche doublement pointée 15/14 14 1/16 7/64
•|... croche triplement pointée 16/15 15 1/15 15/128
• noire 3/2 16 1/12 1/8
•. noire pointée 7/6 24 3/28 3/16
•.. noire doublement pointée 15/14 28 1/8 7/32
•... noire triplement pointée 16/15 30 2/15 15/64
o blanche 3/2 32 1/6 1/4
o. blanche pointée 7/6 48 3/14 3/8
o.. blanche doublement pointée 15/14 56 1/4 7/16
o... blanche triplement pointée 16/15 60 4/15 15/32
O ronde 3/2 64 1/3 1/2
O. ronde pointée 7/6 96 3/7 3/4
O.. ronde doublement pointée 15/14 112 1/2 7/8
O... ronde triplement pointée 16/15 120 8/15 15/16
□ carrée 3/2 128 4/7 1
□. carrée pointée 7/6 192 6/7  
□.. carrée doublement pointée 15/14 224 14/15  
□... carrée triplement pointée 16/15 240 1  

avec
origine : 8 noté •|, constantes (de raison) 3/2 puis 7/6 puis 15/14 puis 16/15, opération : ×, unité : 1

Dans cette suite de 20 valeurs, durées de temps concordent avec intervalles de temps. Cette concordance permet un passage sans heurt d'un chant sans battue à une danse bien battue. L'ajout de 5 valeurs triplement-pointées augmente la suite des durées à 26 durées. Les 5 valeurs triplement pointées seules ont un rapport de 2. Les 5 valeurs doublement pointées seules ont un rapport de 2. Les 5 valeurs pointées seules ont un rapport de 2. Les 5 valeurs non pointées seules ont un rapport de 2. Une durée triplement pointées est à la fois une valeur binaire et une valeur ternaire.

remarque :
Les rapports 15/14 et 16/15 dans le champ des hauteurs harmoniques sont nommés :
demi-ton diatonique majeur et demi-ton diatonique mineur.


plus loin :

5.

L'ajout du quadruple point nous donne une suite de valeurs qui divisent le rapport 2 en 3/2 × 7/6 × 15/14 × 31/30 × 32/31 (où 16/15 = 31/30 × 32/31)

Suite de durées de rapports 3/2, 7/6, 15/14, 31/30 et 32/31
symbole nom rapports valeurs numériques
durées de temps intervalles de temps
• noire 3/2 16 1/12 1/8
•. noire pointée 7/6 24 3/28 3/16
•.. noire doublement pointée 15/14 28 1/8 7/32
•... noire triplement pointée 31/30 30 2/15 15/64
•.... noire quadruplement pointée 32/31 31 15/124 31/128
o blanche 3/2 32 1/6 1/4
o. blanche pointée 7/6 48 3/14 3/8
o.. blanche doublement pointée 15/14 56 1/4 7/16
o... blanche triplement pointée 31/30 60 4/15 15/32
o.... blanche quadruplement pointée 32/31 62 15/62 31/64
O ronde 3/2 64 1/3 1/2
O. ronde pointée 7/6 96 3/7 3/4
O.. ronde doublement pointée 15/14 112 1/2 7/8
O... ronde triplement pointée 31/30 120 8/15 15/16
O.... ronde quadruplement pointée 32/31 124 15/31 31/32
□ carrée 3/2 128 4/7 1
□. carrée pointée 7/6 192 6/7  
□.. carrée doublement pointée 15/14 224 14/15  
□... carrée triplement pointée 31/30 240 30/31  
□.... carrée quadruplement pointée 32/31 248 1  

avec
origine : 16 noté •, constantes (ou de raison) 3/2 puis 7/6 puis 15/14 puis 31/30 puis 32/31, opération : ×, unité ppcm : 1

Dans cette suite de 20 valeurs, durées de temps concordent avec intervalles de temps. Cette concordance permet un passage sans heurt d'un chant sans battue à une danse bien battue. L'ajout de 4 valeurs quadriplement-pointées augmente la suite des durées à 30 durées. Les 4 valeurs quaduplement pointées seules ont un rapport de 2. Les 4 valeurs triplement pointées seules ont un rapport de 2. Les 4 valeurs doublement pointées seules ont un rapport de 2. Les 4 valeurs pointées seules ont un rapport de 2. Les 4 valeurs non pointées seules ont un rapport de 2. Une durée quadruplement-pointées est une valeur binaire (qui ne se divise pas par 3).

remarque :
Les rapports 31/30 et 32/31 dans le champ des hauteurs harmoniques sont nommés :
chroma partiel 31 et 1/4 de ton grecque enharmonique

plus loin :

6.

L'ajout du quintuple point nous donne une suite de valeurs qui divisent le rapport 2 en 3/2 × 7/6 × 15/14 × 31/30 × 61/60 × 62/61 (où 32/31 = 61/60 × 62/61)

Suite de durées de rapports 3/2, 7/6, 15/14, 31/30, 61/60 et 62/61
symbole nom rapports valeurs numériques
durées de temps intervalles de temps
o blanche 3/2 32 1/6 1/4
o. blanche pointée 7/6 48 3/14 3/8
o.. blanche doublement pointée 15/14 56 1/4 7/16
o... blanche triplement pointée 31/30 60 4/15 15/32
o.... blanche quadruplement pointée 61/60 62 15/62 31/64
o..... blanche quintuplement pointée 62/61 63 15/61 61/124
O ronde 3/2 64 1/3 1/2
O. ronde pointée 7/6 96 3/7 3/4
O.. ronde doublement pointée 15/14 112 1/2 7/8
O... ronde triplement pointée 31/30 120 8/15 15/16
O.... ronde quadruplement pointée 61/60 124 15/31 31/32
O..... ronde quintuplement pointée 62/61 126 30/61 61/62
□ carrée 3/2 128 4/7 1
□. carrée pointée 7/6 192 6/7  
□.. carrée doublement pointée 15/14 224 14/15  
□... carrée triplement pointée 31/30 240 30/31  
□.... carrée quadruplement pointée 61/60 248 60/61  
□..... carrée quintuplement pointée 62/61 252 1  

avec
origine : 32 noté o, constantes (de raison) |: 3/2 puis 7/6 puis 15/14 puis 31/30 puis 61/60 puis 62/61 :|×3, opération : ×, unité : 1

Dans cette suite de 18 valeurs, durées de temps concordent avec intervalles de temps. Cette concordance permet un passage sans heurt d'un chant sans battue à une danse bien battue. L'ajout de 3 valeurs quintuplement-pointées augmente la suite des durées à 33 durées. Les 3 valeurs quintuplement pointées seules ont un rapport de 2. Les 3 valeurs quaduplement pointées seules ont un rapport de 2. Les 3 valeurs triplement pointées seules ont un rapport de 2. Les 3 valeurs doublement pointées seules ont un rapport de 2. Les 3 valeurs pointées seules ont un rapport de 2. Les 3 valeurs non pointées seules ont un rapport de 2. Une durée quintuplement pointées est à la fois une valeur binaire et une valeur ternaire.

remarque :
Les rapports 61/60 et 62/61 dans le champ des hauteurs harmoniques n'ont pas de nom :
le rapport 61/60 se rapproche du 1/7e de ton tempéré qui divise l'octave en 42 intervalles égaux

plus loin :

7.

L'ajout du sextuple point nous donne une suite de valeurs qui divisent le rapport 2 en 3/2 × 7/6 × 15/14 × 31/30 × 61/60 × 123/122 × 124/123 (où 62/61 = 123/122 × 124/123)

Suite de durées de rapports 3/2, 7/6, 15/14, 31/30, 61/60, 123/122 et 124/123
symbole nom rapports valeurs numériques
durées de temps intervalles de temps
O ronde 3/2 64 1/3 1/2
O. ronde pointée 7/6 96 3/7 3/4
O.. ronde doublement pointée 15/14 112 1/2 7/8
O... ronde triplement pointée 31/30 120 8/15 15/16
O.... ronde quadruplement pointée 61/60 124 15/31 31/32
O..... ronde quintuplement pointée 123/122 126 30/61 61/62
O...... ronde sextuplement pointée 124/123 127 61/123 123/124
□ carrée 3/2 128 4/7 1
□. carrée pointée 7/6 192 6/7  
□.. carrée doublement pointée 15/14 224 14/15  
□... carrée triplement pointée 31/30 240 30/31  
□.... carrée quadruplement pointée 61/60 248 60/61  
□.... carrée quadruplement pointée 123/122 252 122/123  
□..... carrée sextuplement pointée 124/123 254 1  

avec
origine : 64 noté O, constantes (de raison) |: 3/2 puis 7/6 puis 15/14 puis 31/30 puis 61/60 puis 123/122 puis 124/123 :|×2, opération : ×, unité : 1

Dans cette suite de 14 valeurs, durées de temps concordent avec intervalles de temps. Cette concordance permet un passage sans heurt d'un chant sans battue à une danse bien battue. L'ajout de 2 valeurs sextuplement-pointées augmente la suite des durées à 35 durées. Les 2 valeurs quintuplement pointées seules ont un rapport de 2. Les 2 valeurs quaduplement pointées seules ont un rapport de 2. Les 2 valeurs triplement pointées seules ont un rapport de 2. Les 2 valeurs doublement pointées seules ont un rapport de 2. Les 2 valeurs pointées seules ont un rapport de 2. Les 2 valeurs non pointées seules ont un rapport de 2. Une durée sextuplement-pointées est une valeur binaire (qui ne se divise pas par 3).

remarque :
Les rapports 123/122 et 124/123 dans le champ des hauteurs harmoniques n'ont pas de nom :
les rapports 123/122 et 124/123 sont proches du 1/14e de ton tempéré (84√2) et de l'octave divisé en 85 intervalles égaux (85√2)

plus loin :

8.

L'ajout du septuple point nous donne une suite de valeurs qui divisent le rapport 2 en 3/2 × 7/6 × 15/14 × 31/30 × 61/60 × 123/122 × 247/246 × 248/247 (où 124/123 = 247/246 × 248/247)

Suite de durées de rapports 3/2, 7/6, 15/14, 31/30, 61/60, 123/122, 247/246 et 248/247
symbole nom rapports valeurs numériques
durées de temps intervalles de temps
□ carrée 3/2 128 4/7 1
□. carrée pointée 7/6 192 6/7  
□.. carrée doublement pointée 15/14 224 14/15  
□... carrée triplement pointée 31/30 240 30/31  
□.... carrée quadruplement pointée 61/60 248 60/61  
□.... carrée quadruplement pointée 123/122 252 122/123  
□..... carrée sextuplement pointée 247/246 254 246/247  
□...... carrée septuplement pointée 248/247 255 1  

avec
origine : 128 noté □, constantes (de raison) |: 3/2 puis 7/6 puis 15/14 puis 31/30 puis 61/60 puis 123/122 puis 247/246 puis 248/247 :|×1, opération : ×, unité : 1

Dans cette suite de 8 valeurs, durées de temps concordent avec intervalles de temps. Cette concordance permet un passage sans heurt d'un chant sans battue à une danse bien battue. L'ajout de 1 valeur septuplement-pointées augmente la suite des durées à 36 durées.

remarque :
Les rapports 247/246 et 248/247 dans le champ des hauteurs harmoniques n'ont pas de nom :
ils sont tous deux proche de l'octave divisé en 171 intervalles égaux; le 1/16e divise l'octave en 96...

Arrêtons-nous là; je ne pense pas que la distinction entre □..... = 254 & □...... = 255 soit effective, nous avons des doutes même à partir du quadruple point, mais tout ceci dépend du contexte dans lequel ces spécificités sont exploitées : elles sont là, elles existent. La suite de 30 valeurs (nous nous arrêtons à la valeur de durée 128 = □ au lieu de tendre vers ∞) jusqu'à la O...... = 127, est incluse dans l'ensemble des 128 durées de l'ensemble N (des entiers naturels). L'intersection entre les 30 valeurs usuelles et les 128 données, nous donne 98 valeurs de durées supplémentaires notables en liant les durées de bases. Ce tableau va nous permettre de constater la place des valeurs de durées usuelles par rapport aux valeurs de durées inusuelles.

DU
durées usuelles 		DI
durées inusuelles
•|||| 1    
•||| 2    
•|||. 3    
•|| 4    
    •||•|||| 5 = 4 + 1
•||. 6    
•||.. 7    
•| 8    
    •|•|||| 9 = 8 + 1
    •|•||| 10 = 8 + 2
    •|•|||. 11 = 8 + 3
•|. 12    
    •|.•|||| 13 = 12 + 1
•|.. 14    
•|... 15    
• 16    
    ••|||| 17 = 16 + 1
    ••||| 18 = 16 + 2
    ••|||. 19 = 16 + 3
    ••|| 20 = 16 + 4
    ••||•|||| 21 = 16 + 4 + 1
    ••||. 22 = 16 + 6
    ••||.. 23 = 16 + 7
•. 24    
    •.•|||| 25 = 24 + 1
    •.•||| 26 = 24 + 2
    •.•|||. 27 = 24 + 3
•.. 28    
    •..•|||| 29 = 28 + 1
•... 30    
•.... 31    
o 32    
    o•|||| 33 = 32 + 1
    o•||| 34 = 32 + 2
    o•|||. 35 = 32 + 3
    o•|| 36 = 32 + 4
    o•||•|||| 37 = 32 + 4 + 1
    o•||. 38 = 32 + 6
    o•||.. 39 = 32 + 7
    o•| 40 = 32 + 8
    o•|•|||| 41 = 32 + 8 + 1
    o•|•||| 42 = 32 + 8 + 2
    o•|•|||. 43 = 32 + 8 + 3
    o•|. 44 = 32 + 12
    o•|.•|||| 45 = 32 + 12 + 1
    o•|.. 46 = 32 + 14
    o•|... 47 = 32 + 15
o. 48    
    o.•|||| 49 = 48 + 1
    o.•||| 50 = 48 + 2
    o.•|||. 51 = 48 + 3
    o.•|| 52 = 48 + 4
    o.•||•|||| 53 = 48 + 4 + 1
    o.•||. 54 = 48 + 6
    o.•||.. 55 = 48 + 7
o.. 56    
    o..•|||| 57 = 56 + 1
    o..•||| 58 = 56 + 2
    o..•|||. 59 = 56 + 3
o... 60    
    o...•|||| 61 = 60 + 1
o.... 62    
o..... 63    
O 64    
    O•|||| 65 = 64 + 1
    O•||| 66 = 64 + 2
    O•|||. 67 = 64 + 3
    O•|| 68 = 64 + 4
    O•||•|||| 69 = 64 + 4 + 1
    O•||. 70 = 64 + 6
    O•||.. 71 = 64 + 7
    O•| 72 = 64 + 8
    O•|•|||| 73 = 64 + 8 + 1
    O•|•||| 74 = 64 + 8 + 2
    O•|•|||. 75 = 64 + 8 + 3
    O•|. 76 = 64 + 12
    O•|.•|||| 77 = 64 + 12 + 1
    O•|.. 78 = 64 + 14
    O•|... 79 = 64 + 15
    O• 80 = 64 + 16
    O••|||| 81 = 64 + 16 + 1
    O••||| 82 = 64 + 16 + 2
    O••|||. 83 = 64 + 16 + 3
    O••|| 84 = 64 + 16 + 4
    O••||•|||| 85 = 64 + 16 + 4 + 1
    O••||. 86 = 64 + 16 + 6
    O••||.. 87 = 64 + 16 + 7
    O•. 88 = 64 + 24
    O•.•|||| 89 = 64 + 24 + 1
    O•.•||| 90 = 64 + 24 + 2
    O•.•|||. 91 = 64 + 24 + 3
    O•.. 92 = 64 + 28
    O•..•|||| 93 = 64 + 28 + 1
    O•... 94 = 64 + 30
    O•.... 95 = 64 + 31
O. 96    
    O.•|||| 97 = 96 + 1
    O.•||| 98 = 96 + 2
    O.•|||. 99 = 96 + 3
    O.•|| 100 = 96 + 4
    O.•||•|||| 101 = 96 + 4 + 1
    O.•||. 102 = 96 + 6
    O.•||.. 103 = 96 + 7
    O.•| 104 = 96 + 8
    O.•|•|||| 105 = 96 + 8 + 1
    O.•|•||| 106 = 96 + 8 + 2
    O.•|•|||. 107 = 96 + 8 + 3
    O.•|. 108 = 96 + 12
    O.•|.•|||| 109 = 96 + 12 + 1
    O.•|.. 110 = 96 + 14
    O.•|... 111 = 96 + 15
O.. 112    
    O..•|||| 113 = 112 + 1
    O..•||| 114 = 112 + 2
    O..•|||. 115 = 112 + 3
    O..•|| 116 = 112 + 4
    O..•||•|||| 117 = 112 + 4 + 1
    O..•||. 118 = 112 + 6
    O..•||.. 119 = 112 + 7
O... 120    
    O...•|||| 121 = 120 + 1
    O...•||| 122 = 120 + 2
    O...•|||. 123 = 120 + 3
O.... 124    
O..... 125    
O...... 126    
O....... 127    
□ 128    

Les durées entières et pointées tiennent une place singulière, mais régulière :
les espaces entre ces valeurs se présentent comme tels :

DU : durées usuelles 4   3   1 - 3   1 - 1 - 3   1 - 1 - 1 - 3   1 - 1 - 1 - 5 = 30
DI : durées inusuelles   1   3 - 1   7 - 3 - 1   15 - 7 - 3 - 1   31 - 15 - 7 - 3   = 98

. Le nombre de valeurs de durées inusuelles de 98 contre un nombre de 30 valeurs de durées usuelles, questionnent. Les 98 valeurs de l'inusualités se positionnent par rapport aux 30 valeurs de l'usualité. La facilité d'interprétation est un argument en faveur de l'usualité contrairement à la complexité d'interprétation de l'inusualité. Dans les deux cas, un contexte d'utilisation possible doit être proposé par le compositeur.

. Les valeurs de durées pointées se ressèrent vers la valeur de durée supérieure dû aux divisions des plus petits rapports en deux suivant la suite des rapports des entiers naturels tels que : 1, 2, 3/2, 4/3, 5/4, 6/5, 7/6, 8/7, 9/8, , etc. dont voici la suite : 3/2 × 7/6 × 15/14 × 31/30 × 61/60 × 123/122 × 247/246 × 248/247 constituée de 8 rapports.

...

 

 

Comment noter le passage entre la chronologie de la danse et les durées indépendantes du chant ?

suite

re tour à la table des matières