
naissance de la polyphonie occidentale dans la musique
Définitions (avant lecture)
Prolation (nom féminin), terme plus en usage qui désigne la « division par deux ou par trois de la semi-brève (l'équivalent de la ronde actuelle). La prolation était dite mineure lorsque la semi-brève était divisée en 2 minimes (l'équivalent de deux blanches actuelles). La prolation était dite majeure lorsqu'on divisait cette figure de note en 3 minimes » (https://fr.wiktionary.org/wiki/prolation). Le terme équivalent dans la notation italienne du XIVe siècle est « divisio ». (https://en.wikipedia.org/wiki/Prolation).
Sesquialtère (nom latin de) : la quinte (~XVIe siècle).
Les 3 musiques. Boèce (470-525) divise la musique en 3 catégories dans son Institution musicale (510) : la musique de l'univers (celle qui s'occupe des proportions des objets célestes), la musique de l'homme (celle qui s'occupe des liens de l'âme et du corps) et la musique instrumentale (celle qui s'occupe des sons). Cette distinction est encore vivace au XIVe siècle à ce que Philippe de Vitry doit préciser de quelle musique il parle dans son traité Ars Nova.
ARS NOVA
app. 1320
[traduit du Latin par André Gilles, Jean Maillard]
[texte avec les schémas]
PHILIPPE DE VITRY
ARS NOVAChapitre I
Les trois espèces de musiqueIl y a trois espèces de musique : la musique de l'univers, celle de l'homme et la musique instrumentale. C'est de la musique instrumentale qu'il s'agit ici.
Est dite musique instrumentale toute musique obtenue sur des instruments tels que la cithare, la vièle ou le monocorde : c'est de lui seul qu'il est ici question.
Le monocorde est un instrument pourvu d'une seule corde, dont le jeu s'établit selon les trois genres diatonique, chromatique et enharmonique. Il s'agit ici du diatonique.Chapitre II
Les treize intervalles de la musiqueEst diatonique tout ce qui procède par série de deux tons et un demi-ton. 13 intervalles sont dans ce cas.
Le premier est, musicalement, l'unisson, qui réalise numériquement une unité, comme 1 par rapport à 1. Le second est, musicalement, l'octave qui, numériquement, représente le double, comme 2 par rapport à 1. Le troisième est, musicalement, la quinte, qui est, numériquement, sesquialtère, comme 3 par rapport à 2. Le quatrième est, musicalement, la quarte, qui est numériquement, sesquitierce, comme 4 par rapport à 3. Le cinquième est le ton qui est sesquioctave comme 9 par rapport à 8. Le sixième est la tierce mineure, dont l'expression numérique enferme 27 plus 5, comme le rapport 32 à 27. Le septième est la tierce majeure, dont l'expression numérique enferme 64 plus 17, comme le rapport 81 à 64. Le huitième est le demi-ton, dont l'expression numérique enferme 243 plus 13, comme le rapport 256 à 243. Le neuvième est la sixte mineure, dont l'expression numérique enferme 81 plus 47, comme le rapport 128 à 81. Le dixième est la sixte majeure, dont l'expression numérique enferme 32 plus 22, comme le rapport 54 à 32. Le onzième est la septième mineure, dont l'expression numérique enferme 9 plus 7, comme le rapport 16 à 9. Le douzième est la septième majeure, dont l'expression numérique enferme 256 plus 230, comme le rapport 486 à 256. Le treizième est le triton, dont l'expression numérique enferme 512 plus 217, comme le rapport 729 à 512.Chapitre III
Toute inégalité procède de l'égalitéToute inégalité procède de l'égalité, ce qui se voit si l'on prend trois unités, c'est-à-dire une série de termes égaux, et qu'on les dispose en un lieu donné. Suit cette règle que si l'on prend une quantité égale au premier terme et qu'on la pose en premier lieu, puis qu'on prenne une quantité égale au premier et au second, et qu'on la pose ensuite, puis qu'on prenne une quantité égale au premier, plus deux fois le second, plus une quantité égale au troisième, et qu'on la place en troisième position, on obtient alors la série des doubles, qui représente la première espèce des multiples. Et, en procédant ainsi, on obtient à partir de la série des doubles la série des triples, et ainsi de suite : rapports doubles 1, 2, 4 ; triples 1, 3, 9 ; quadruples 1, 4, 16 ; et ainsi, par paliers, de 1 jusqu'à la fin, toute inégalité procède de l'égalité. Voilà qui suffit en ce qui concerne les multiples [1].
Chapitre IV
Etude des rapports (proportions)D'un rapport du simple au double on tire, en inversant les termes, un nombre qui en contient un autre plus sa moitié. D'un rapport du simple au triple, on tire un nombre qui en contient un autre plus le tiers, et ainsi des autres espèces.
Rapports du simple au double, en ordre inverse 4 2 1 Rapport sesquialtère 4 6 9 D'un nombre qui en contient un autre plus sa moitié on tire, en inversant les termes, un nombre qui en contient un autre plus les deux tiers. De même, d'un nombre qui en contient un autre plus le tiers, on tire, en inversant les termes, un nombre qui en contient un autre plus les trois quarts, etc.
Rapport sesquialtère en ordre inverse 9 6 4 Rapport superbipartiel 9 15 25 D'un nombre qui en contient un autre plus sa moitié, on tire un autre nombre, au multiple supérieur, qui est double et sesquialtère, sans inverser les termes, etc.
Rapport sesquialtère 4 6 9 Rapport à la fois double et sesquialtère 4 10 25 D'un nombre qui en contient un autre plus les deux tiers, on tire un autre nombre, au multiple supérieur, sans inverser les termes, qui est double et superbipartiel.
Rapport superbipartiel 9 15 25 Rapport à la fois double et superbipartiel 9 24 64 Si on multiplie (les deux termes d') un rapport par le même nombre, on obtiendra toujours le même rapport.
Rapport sesquialtère 3 2 Le même rapport sesquialtère 6 4 Si l'on veut, à partir d'une proportion, en établir deux, on multiplie le premier terme par lui-même, le second par lui-même, puis le premier terme du rapport initial par le second, et l'on obtient le « moyen ».
Rapport sesquialtère 9 4 Moyen 6 Rapport sesquialtère 3 2 Si l'on veut trouver l'intervalle qu'il y a entre deux rapports, on écrit les rapports choisis de façon que le premier terme de l'un soit, sous le premier terme de l'autre, le deuxième terme de l'un sous le deuxième terme de l'autre, puis l'on multiplie en croix, le premier terme de l'un, au-dessus, par le deuxième terme le l'autre, au-dessous ; le second terme de l'un, au-dessus, par le premier terme de l'autre, au-dessous, et l'on obtient le résultat cherché.
Ton (tonus) 9 8 Quinte (diapente) 3 2 Quarte (diatessaron) 4 3 Chapitre V
Les rapports musicaux sur le monocordeSi la longueur d'une corde se trouve réduite, le son qu'elle rend devient plus aigu, ou encore s'élève, et il faut savoir que toute moitié de corde donne un son identique mais à l'octave du son fondamental de la corde entière. Il y a deux principes à observer : à un son semblable répond un signe semblable ; à des sons différents, des signes différents. Il faut également savoir que deux quartes et un ton, ou une quarte et une quinte font une octave ; qu'une tierce majeure plus un demi-ton font une quarte.
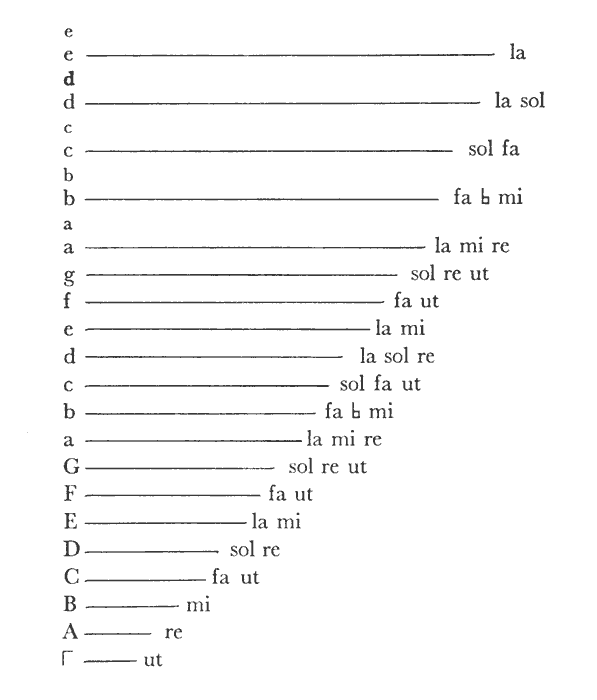
Ainsi, pour réaliser sur une corde donnée toutes les espèces de rapports musicaux selon le genre diatonique, il faut d'abord poser un ton, puis un autre ton, ensuite un demi-ton, de Γ à G8, que l'on appelle fin de la première succession diatonique, du fait de la confusion des états ; puis, de G8 à g15 en procédant de la même manière ; ensuite de g 15 jusqu'à 20 et au-delà si le registre est plus étendu, mais ce n'est pas dans nos habitudes [2]. Pour que la chose soit plus nette, voir la figure.t t s t t s t t s s t t s t t s s t t
Γ A B C D E F G ab-b c d e f g ab-b c d e
t' t'Chapitre VI
Détermination (des rapports) sur le monocorde [3]Voyons maintenant comment on détermine ces rapports musicaux sur le monocorde.
Soit une corde qui, prise dans toute sa longueur, donne Γ : sa moitié G la moitié de sa moitié g. Aux trois quarts de Γ se place C dont la moitié sera c et la moitié de sa moitié cc. Aux trois quarts de C se place F dont la moitié sera f, la moitié de f donnant ff. Les deux-tiers de Γ donnent D dont la moitié sera d, la moitié de d donnant dd. Si on divise D par trois, qu'on porte ce tiers vers Γ, on obtient A, dont la moitié donne a, et la moitié de la moitié aa. Les deux tiers de A donnent E, dont la moitié donne e et la moitié de sa moitié ee. Si l'on divise E par trois, et qu'on porte ce tiers vers Γ on obtient B, dont la moitié est b, et la moitié de sa moitié bb. Les trois quarts de F donnent b, dont la moitié donne bb, et la moitié de la moitié donne bbb.
Ceux de ces signes qui vont de Γ à G sont dits graves parce qu'ils traduisent une sonorité grave ou très basse, et sept, aigus, parce qu'ils traduisent une sonorité aiguë. Quant aux derniers, ils sont dits suraigus parce qu'ils se placent au-dessus des aigus, ou parce qu'ils traduisent un son suraigu, c'est-à-dire très aigu.
On peut former de ces sept signes du monocorde, G, A, B, C, D, E, F, une série indéfinie. D'autre part selon notre usage, il y a six noms de notes, soit ut, ré, mi, fa, sol, la, que l'on dispose au-dessus des signes énumérés précédemment, de sorte qu'à G, C, F, réponde un ut, et aux signes suivants, les notes suivantes. Voilà en quoi consiste la « compositio » de la gamme. La gamme n'est donc rien d'autre que la corrélation établie entre les signes du monocorde et les notes ; ceci apparaitra plus clairement dans la figure suivante.
illustration de la traduction (vertical) :  |
illustration de la version latine (ou diagonal) :  |
= peu importe |
Chapitre VII
Les différentes parties de la musiqueIl y a quatre parties principales dans l'étude de la musique ou de la gamme. La première traite des signes et des noms des notes ; la seconde des lignes et des interlignes ; la troisième des propriétés ; la quatrième des mutations.
Chapitre VIII
Lignes et interlignesIl a été question des signes et des noms des notes. Nous allons traiter maintenant des lignes et interlignes.
La ligne et l'interligne, au sens où on les entend ici, correspondent au pair et à l'impair. Tout ce qui est sur une ligne est dit impair ; ce qui est dans l'interligne est dit pair. Il s'ensuit que tout signe qui répond à un nombre impair est sur une ligne, et tout signe qui répond à un nombre pair dans un interligne. Ainsi, selon l'ordre naturel des nombres, si le premier signe se trouve sur une ligne, le suivant sera dans un interligne, et, vice versa. Au-delà s'opposent au premier tout quatrième et huitième signes, mais, en huitième position, se retrouve un signe semblable. Donc, si le premier se trouve sur une ligne, le suivant sera dans un interligne, et vice versa. Ce système se trouve représenté, conformément à la quadrature, c'est-à-dire aux lignes tracées dans la « manus », entre la quatrième et la première lignes.Chapitre IX
Les « propriétés » musicalesLa propriété n'est autre chose qu'un caractère spécifique. Il y en a trois sortes : (l'état) bécarre, (l'état) naturel et (l'état) bémol. B carré se place un ton au-dessus de A, a et aa ; et b mol se place un demi-ton au-dessus de a et aa.
La mélodie qui n'a pas besoin de B, c'est-à-dire qui n'implique aucun son mobile, est dite naturelle.
Règle : Tout ut en G est en état bécarre, ainsi que les notes suivantes de l'hexacorde ; tout ut en C est en état naturel ; tout ut en F est en état bémol. D'où les vers :
C naturam dat, F b molle tibi signat,
G quoque b durum te semper habes caniturum.
C indique l'état naturel, F l'état b mol ; G, quant à lui, invite à chanter en b dur. Et en voilà assez sur les propriétés musicales.Chapitre X
Les mutationsUne mutation n'est autre chose que l'abandon d'un nom de note au profit d'un autre, le son et le signe demeurant les mêmes. Il s'ensuit que, partout où se fait une mutation, il faut qu'il y ait au moins deux notes.
Or, en gamma ut, A ré, B mi et e la, il n'y a qu'un nom de note. Il n'y a donc pas de mutation. Il n'y en a pas non plus en b fa b mi, parce qu'il y a là des signes différents, et des notes différentes ; et, parce qu'elles ne se placent pas sous les mêmes signes, elles ne répondent pas non plus à la même sonorité : ainsi ne peut-il y avoir de mutation, car cela irait contre la définition. Si en effet elles répondaient à la même sonorité, on devrait dire b fa mi.
Et, pour que tout le monde comprenne plus aisément, qu'on regarde sur le monocorde.
Là où il y a deux notes, il y a deux mutations, comme en F fa ut, où l'on dit fa ut, ut fa. Autrement, là où il y a trois notes, il y a six mutations, comme en G sol ré ut et ailleurs, puisque, là où il y a deux notes, la première se change en la seconde et vice versa, et que là où il y en a trois la première se change en la seconde et vice versa ; en la dernière et vice versa ; la seconde en la dernière et vice versa. Ainsi, là où il y a deux (notes), elles ne se dédoublent pas en quatre (mutations), comme trois (notes) se dédoublent en six (mutations).
Règle : Toute mutation qui s'achève sur ut ré mi est dite ascendante, parce qu'elle permet de monter plus que de descendre ; et toute mutation qui s'achève sur fa sol la est dite descendante parce qu'elle permet de descendre plus que de monter. On procède à une mutation, pour monter ou pour descendre, ainsi qu'on le voit en C fa ut, puisque, si l'on y mettait fa, on pourrait monter jusqu'à la troisième note ; mais, si l'on voulait porter une quatrième note, il faudrait mettre ut en C fa ut, ce qui constitue une mutation de fa en ut ; et, en descendant, on peut appliquer le même principe, à son gré. Ces indications sont suffisantes.Chapitre XI
Définition de la musiqueSachez que la musique est la science du chant juste, c'est-à-dire le moyen facile de parvenir à chanter parfaitement. Etymologiquement, moys, c'est-à-dire eau, et ycos, c'est-à-dire science, parce qu'elle a été découverte au bord des eaux. Elle connaît treize intervalles : l'unisson, le ton, le demi- ton, etc.
Chapitre XII
L'unissonEst unisson tout ce qui se trouve sur une même ligne de chant ou dans un même intervalle, et ceci en tout endroit de la gamme, c'est-à-dire quel que soit le signe ou la note de la gamme. Etymologiquement, un et son, l'unisson offrant un seul et même son, selon sa figuration et sa sonorité propres.
D'une façon différente, est dit unisson le son rendu par une seule note dont on ne s'écarte pas ; il sera toujours en effet sur une même ligne ou dans un même interligne. Mais si on s'écarte d'une note donnée en touchant la voisine, on réalise alors tantôt un ton, tantôt un demi-ton. Il faut savoir toutefois que l'unisson ne constitue pas par lui-même une consonance, mais est le principe des autres consonances, et, sans l'unisson, il ne saurait y avoir de consonance.
Qu'est-ce que l'unisson ? C'est la note sur laquelle on attaque le chant ; cette note ni ne monte, ni ne descend, et elle peut, au gré du chanteur, être placée soit dans un registre élevé, soit dans un registre grave, et on la fixe dans la clé qui conviendra le mieux.Chapitre XIII
Le demi-tonLe demi-ton est, entre deux unissons, un espace que, conformément aux possibilités de la voix humaine, il n'est ni loisible ni possible de diviser ; autrement dit, qui ne souffre pas de son intermédiaire. Il se trouve entre b carré et c, ou encore entre e et f, ou encore a et b rond sans qu'il y ait place entre ces signes pour une autre note, naturellement une fois établie la suite naturelle des notes, puisque, entre f et e il y a une septième majeure. Mais si, parmi les noms de notes, on considère mi fa, il y a la même distance qu'entre les signes corrélatifs, cela va sans dire. « Semitonium » ne vient pas (en effet) de « semis », c'est-à-dire moitié, comme le pensent certains, puisqu'il vaut moins que la moitié d'un ton, comme cela se voit sur l'échelle du monocorde, mais de « semus-ma-mum », c'est-à-dire imparfait, comme s'il s'agissait d'un son imparfait.
Le demi-ton, comme le dit Bernard, est l'adoucissement et l'agrément le la mélodie tout entière, et sans lui elle serait gâtée, elle perdrait son caractère, il n'en resterait rien.
Boèce, de son côté, indique, en traitant de la question, la valeur du demi-ton.Chapitre XIV
La musique fausseIl arrive en effet parfois que, par musique « fausse », nous faisons un demi-ton là où il ne doit point y en avoir ; en musique mesurée, nous voyons en effet que le ténor d'un motet ou d'un rondeau se trouve sur b fa b (carré) mi, dans l'état b (carré) dur : alors il faut que le déchant qu'il admet à la quinte supérieure dise mi sur f aigu, et ceci par musique fausse. En effet, une quinte mi fa ne constitue pas une bonne concordance parce que, du b carré à f aigu, il y a deux tons et deux demi-tons, dont le groupement ne correspond pas à une consonance : or il faut, là où il y a une quinte entre une note et me autre, qu'il y ait une bonne et vraie consonance.
De là par conséquent naît évidemment la question de savoir quelle nécessité il y a d'introduire dans la musique régulière la musique fausse ou fausse mutation, alors que ce qui est régulier ne doit rien admettre qui soit faux, mais vrai bien plutôt. A quoi il faut répondre que la fausse mutation, ou musique fausse, loin d'être inutile, est nécessaire pour obtenir une bonne consonance, et en éviter une mauvaise. Comme il a été dit en effet, si on veut avoir une quinte, il faut nécessairement avoir trois tons et un demi- on, et si une figure (de note) est sur b fa b (carré) mi en b carré, et qu'une autre soit sur f fa ut aigu, état naturel, il n'y a pas consonance, parce qu'il n'y a pas là trois tons et un demi-ton, mais seulement deux tons et deux demi-tons. Toutefois, on peut ici même réaliser la consonance, ce qu'on nomme « par musique fausse », c'est-à-dire quand on fait un ton d'un demi-ton et vice versa : en fait, il ne s'agit pas de musique fausse, mais irrégulière [4].
On notera que b fa b (carré) mi ne relève pas du même principe que les autres clés. On le reconnaît grâce 'à un 6 carré ou à un b rond qu'on place en un lieu inusité, en sorte qu'on dise, avec un b carré, mi dur en f aigu, ou, l'on met un b rond sur b fa b (carré) mi (ou telles autres clés semblables), qu'I détermine un intervalle égal à un ton : alors il y a un intervalle de quinte. Ainsi la musique fausse est maintes fois nécessaire, afin que toute consonance ou mélodie, grâce à l'un ou l'autre signe, soit rendue parfaite.
Selon ce qui a été dit il faut donc savoir qu'il y a deux signes de nuque fausse : le b rond et cette autre figure : b carré ; ils ont la propriété suivante : b rond fera d'un demi-ton un ton, en descendant, et d'un ton un demi-ton, en montant ; le contraire se produit avec cette autre figure b (carré) : d'un ton, en descendant, on fera un demi-ton, et d'un demi-ton, en montant, on fera un ton. Cependant, là où ces signes se justifient, ils sont, comme il a été dit plus haut, non pas faux, mais justes et nécessaires, car sans eux, aucun motet ou rondeau ne peut se chanter. Ainsi donc ils sont justes, puisque, si quelque chose est faux, cela entraîne que ce n'est point juste ; or ce qui nous occupe n'est point faux. Donc....(en marge du ms) Note sur la tierce mineure [5] :
Il semble qu'elle doive plutôt contenir deux tons et demi qu'un ton demi, parce que le diton, de soi, contient deux tons. Si donc on en ajoute un demi, il semble qu'il y ait ici deux tons et demi (ou demi-ton). II fi répondre en invoquant cette règle : quand, dans l'arrangement des nombres, le plus petit précède le plus grand, comme dans XIV - I devant V - faut ôter une unité du plus grand. De même pour le semiditon.Chapitre XV
Les notes et leur valeurSix minimes peuvent constituer un temps imparfait. A noter que, pour imparfait, quand il y a deux semi-brèves sans queues, les deux ont la même valeur, et chacune vaut trois minimes. Ex. :
Quand il y en a trois, la première vaut trois minimes, la seconde deux, la troisième une seule. Ex. :
Quand il y en a quatre, la première est une mineure, la seconde une minime, la troisième une mineure, la quatrième une minime. Ex. :
Quand il y en a cinq, les trois premières sont des minimes, la quatrième une mineure, la cinquième une minime. Ex. :
Quand il y en a six, elles sont toutes égales et valent une minime. Ex. :
C'est ainsi que doivent être comptées toutes les semi-brèves en temps parfait ou imparfait, quand elles n'ont pas de queues. Si elles en possèdent, elles doivent en effet être comptées en conséquence. A noter qu'il ne peut y en avoir plus de six pour un temps imparfait, à moins que dans ce cas elles ne soient semiminimes. Ex. :
Selon certains, les valeurs de ces semi-brèves reçoivent une dénomma- 1m propre. La semi-brève qui vaut six minimes s'appelle majeure; la semi-brève qui en vaut cinq ou quatre s'appelle semi-majeure, de « semusa-um », c'est-à-dire imparfait. Celle qui vaut trois minimes s'appelle normale, bien que toutes les figures en losange, au sens large du mot, c'est-à-dire quand il s'agit des semi-brèves, portent le nom de semi-brèves. Celle qui vaut deux minimes s'appelle mineure, comme il a été dit plus haut. Celle qui n'en vaut qu'une s'appelle minime. Celle qui vaut la moitié d'une minime s'appelle semiminime.
D'autres noms pourraient être donnés à la minime et a la semiminime, à l'intérieur du « gradus » [6] où se rencontre la minime : on appellera alors la minime semimineure, et la semiminime minime.
Selon les modernes, de même qu'une minime peut être diminuée, de même elle peut être augmentée. Ainsi, quand deux minimes se trouvent entre deux semi-brèves ou deux brèves la seconde minime en vaut deux, et s'appellera « minima altéra », du moins dans un « degré » ternaire; de même quand deux semi-brèves se trouvent entre deux brèves, en mode ternaire (ou parfait), la seconde semi-brève se dénommera « altera » et vaudra six minimes comme il a été dit plus haut.Chapitre XVI
Les signes des temps parfaits et imparfaitsUne fois traitée la question des brèves et des semi-brèves, des minimes et des semi-minimes, et de leur valeur, il faut parler des signes des temps parfaits et imparfaits. Ainsi pour indiquer un temps parfait, on met un petit cercle rond parce que la forme ronde est parfaite; il arrive aussi, selon certains, qu'on mette trois petits traits obliques [7] : cela revient au même. Ex. :
Pour faire comprendre que toute semi-brève se divise en trois parties égales en un passage ternaire, il faut dire que partout où se trouve un tel cercle, ou trois traits sans point de division, cela signifie perfection, c'est-à-dire que le temps, quant à lui, est parfait, puisque essentiellement divisible en trois parties égales.
Qu'il soit parfait se prouve ainsi. Est parfait ce qui a un commencement, un milieu et une fin. Or le temps parfait présente ce caractère. Donc .... etc.
Inversement, est imparfait ce qui ne possède point ces éléments, ou est privé de l'un d'entre eux. Or le temps imparfait présente ce caractère. Donc .... La majeure est évidente. La mineure s'explique: en effet, le temps imparfait ne se divise qu'en deux parties, et manque ainsi d'un des éléments (qui font la perfection). On se servira, pour signaler l'imperfection, d'un demi-cercle, ou de deux petits traits.Chapitre XVII
Les changements de mode et de temps parfaits et imparfaitsAprès avoir fait une étude complète des signes qui indiquent les changements de temps, il nous faut, pour qu'on n'ait rien à y ajouter, dire que chez les musiciens modernes le changement se fait à la fois en mode et en temps. Il y a des textes musicaux parfaits en mode et temps; d'autres imparfaits; d'autres sont parfaits en mode, non en temps; d'autres inversement; d'autres présentent des passages parfaits à la fois en mode et en temps, d'autres des passages imparfaits. Et, afin de connaître de façon précise la façon dont varient temps et mode, nous convenons de signes déterminés pour le temps parfait et le temps imparfait. Mais parlons d'abord des différentes modifications des textes musicaux.
Le mode s'appelle parfait quand il admet trois temps - parfaits ou imparfaits - qui constituent une perfection. Mais il s'appelle imparfait quand il en admet deux. En mode parfait, une longue devant une longue vaut toujours trois temps, à moins qu'elle ne soit rendue imparfaite par une brève isolée, avant ou après. La double longue vaut six temps. Mais en mode imparfait, une longue simple vaut deux temps. Elle n'en vaut jamais trois, à moins qu'on n'y ajoute un point de division. La double longue, quant à elle, en vaut quatre, et ne peut être augmentée; elle ne peut d'autre part être diminuée que par une ou deux minimes. Ex.:En mode parfait, comme on l'a vu, la double longue est rendue imparfaite de deux façons: ou par une brève seule, et alors elle ne vaut que cinq temps; ou par deux, et elle n'en vaut que quatre. Elle pourrait l'être aussi par des minimes, comme la double longue imparfaite. De plus, en mode parfait, la seconde de deux brèves placées entre deux longues devient "altera", comme on l'a vu dans l'ancienne méthode. Mais en mode imparfait, aucune ne peut ni ne doit le devenir.
En mode parfait, les pauses sont "entières", c'est-à-dire en une seule figure, mais non en mode imparfait. En mode parfait on ne doit pas faire de grandes pauses de deux temps en une seule figure. Ainsi, toutes les fois que l'on rencontre des pauses de trois temps en une seule figure, le mode est parfait, comme dans ORBIS ORBATUS. Chaque fois que se rencontrent deux ou plusieurs pauses successives, dont chacune vaut deux temps, le mode est imparfait, comme dans le motet ADESTO SANCTA TRINITAS.
Mode et temps parfaits se rencontrent ensemble dans le motet qui s'appelle DEUS JUDEX FORTIS [8]. Le mode est parfait parce qu'il admet toujours trois temps pour constituer une perfection. Le temps est parfait parce que chaque temps se divise en trois semi-brèves égales. Mais le mode est imparfait et le temps imparfait dans le motet ADESTO. Le mode est imparfait puisque deux temps y sont reçus (pour une perfection); le temps est imparfait puisque chaque temps ne se divise qu'en deux semibrèves égales.
Il y a mode parfait en temps imparfait dans BONA CONDIT. On a vu plus haut ce qui fait le mode parfait et le temps imparfait. Le temps est parfait et le mode imparfait dans MISERA PER LICONIA [9]. Le temps est tantôt parfait, tantôt imparfait, et le mode de même dans le motet GARISON SELON NATURE. Et voilà qui suffit en ce qui concerne la division du temps et du mode.1 Chapitre XVIII
Les signes des modes et temps parfaits et imparfaits2 Pour indiquer le mode parfait, on porte, selon certains, un petit carré qui contient trois petits traits élongés. Ex.:
3 Pour indiquer le mode imparfait, on porte un petit carré qui contient deux petits traits élongés. Ex.:
4 Pour indiquer simultanément mode et temps parfaits, on portera un cercle contenant trois traits, le cercle pour indiquer le temps parfait, les traits le mode. Ex.:
5 Pour indiquer mode et temps imparfaits, on portera un demi-cercle contenant deux traits. Ex.:
6 Mais pour modifier le mode seul sans le temps, nous y attribuerons le signe qui lui est spécifique, c'est-à-dire le petit carré.
Chapitre XIX
Les notes rougesVoyons rapidement, du moins pour ne pas sembler méconnaître ce point, pourquoi on utilise des notes rouges dans les motets. Il faut dire qu'il y a à cela deux raisons principales: ou bien les rouges se chantent dans une autre mesure que les noires, comme dans THOMA TIBI OBSEQUA: c'est pourquoi, au ténor de ce motet, les rouges se chantent par temps parfaits en mode imparfait, les noires inversement. On utilise aussi parfois des rouges parce qu'elles passent sous un mode différent, comme dans le motet IN ARBORIS EMPIRO: au ténor de ce motet, les rouges indiquent qu'il faut admettre trois temps pour constituer une perfection, mais les noires deux; ou bien on utilise des rouges ici et là, dans des ballades, des rondeaux et des motets parce qu'elles se regroupent pour pouvoir entrer en compte avec d'autres perfections, comme dans PLURES ERRORES [10]
D'une seconde manière on utilise les notes rouges parce que les endroits où elles se trouvent se chantent en réalité à l'octave, comme dans GRATIA MISERI et dans le motet qui s'intitule QUANT AMORS. Au ténor de ces motets, toutes les notes rouges se chantent à l'octave.
Parfois les notes rouges s'utilisent pour indiquer un changement dans le chant naturel, c'est-à-dire le chant simple, le plain-chant, parce que tout se passe comme si l'on n'était pas dans le plain-chant, c'est-à-dire dans le chant naturel, comme dans CLAERBURG. Parfois les notes rouges sont utilisées par endroits pour ôter à une longue placée devant une longue sa valeur de trois temps, ou pour que la seconde de deux brèves placées entre deux longues ne soit nulle part rendue "altéra", comme dans le ténor de IN NOVA FERT ANIMUS. On les utilise aussi pour donner à une longue devant une longue la valeur de trois temps, à une brève devant une brève la valeur de trois semi-brèves, comme dans IN ARBORIS.
On utilise aussi parfois des notes rouges parce que mode et temps varient, comme dans le ténor de GARISON: dans le ténor de ce motet, les noires longues valent en effet trois temps parfaits, et les rouges, deux temps imparfaits; parfois c'est l'inverse, comme dans le ténor du motet qui s'intitule PLURES ERRORES SUNT.Chapitre XX
Les dénominations des temps parfaits
Le petit temps parfaitComment temps et prolation se divisent en six ou neuf minimes, noie en avons traité plus haut, là où il convenait. Pour ne pas donner l'un- pression que nous n'avons pas fait une étude sérieuse de la division des temps, nous voulons en traiter plus rigoureusement.
Le temps parfait offre trois aspects: il y a le petit temps parfait, le temps parfait moyen, le grand temps parfait. Francon a utilisé le petit temps parfait. Selon Maître Francon, et comme il a été vu plus haut, le petit temps parfait ne contient que trois semi-brèves qui sont si réduites qu'elles ne peuvent pas être divisées en valeurs plus grandes que des semiminimes. A noter que, quand on rencontre un texte musical en temps parfait où il n'y a que trois semi-brèves pour un temps, elles doivent être comptées selon le petit temps parfait; (s'il y en a quatre, les deux premières sont des semiminimes, sauf indication contraire).
Ajoutons que quand deux semi-brèves représentent ce petit temps parfait, la première doit être majeure, et jamais la seconde, sauf indication particulière, bien que, dans l'esprit de l'ancienne méthode, nous ayons prouvé que la seconde devait être majeure. La raison en est que ces semi-brèves se comptent en petit temps parfait comme trois minimes en grand temps parfait. En effet, quand deux semi-brèves sont mises pour trois minimes, la première vaut deux minimes, la seconde n'en vaut qu'une, sauf indication contraire, comme on l'a vu plus haut.Chapitre XXI
Le temps parfait moyenLe temps parfait moyen contient trois semi-brèves de valeur égale, dont chacune vaut deux minimes ou l'équivalent; et le temps parfait moyen ne contient que six minimes; si on met quatre (semi-brèves), deux doivent être des minimes; si on en met cinq, quatre doivent devenir minimes; si on en met six, toutes seront des minimes et auront même valeur. Et si on les divise, on les divisera en semiminimes, chaque minime se divisant en deux semiminimes. Quand donc on voit qu'on ne met pas plus de six semibrèves par temps, on doit les compter selon le temps parfait moyen. On peut toutefois les compter selon le grand temps, bien qu'il n'y en ait pas plus de six, ceci quand elles sont dépourvues de queues. Si elles portent de ces signes, il convient en effet d'en tenir compte dans la détermination de leur valeur.
Chapitre XXII
Le grand temps parfaitIl contient trois semi-brèves dont chacune vaut trois minimes, et ainsi le grand temps parfait contient neuf minimes et n'en pourrait valoir plus, sauf à être divisé en semiminimes. Quand donc on met plus de six semibrèves, il faut nécessairement qu'il y ait grand temps parfait, et ainsi le grand temps parfait contient trois minimes pour un temps.
Chapitre XXIII
Les dénominations des temps imparfaits
Le petit temps imparfaitIl faut savoir que, comme le temps parfait est triple, soit petit, moyen et grand, ainsi qu'il a été dit, de même le temps imparfait offre deux aspects: le petit temps imparfait et le grand. Le petit temps contient deux semi-brèves dont chacune vaut deux minimes, et ainsi le petit temps imparfait ne doit valoir que quatre minimes, sauf à être divisé en semiminimes.
Chapitre XXIV
Le grand temps imparfaitLe grand temps imparfait contient deux semi-brèves de valeur égale, doit chacune vaut trois minimes; ainsi le grand temps imparfait contient-il six minimes. Quand donc on voit qu'on met plus de quatre minimes pour un temps imparfait, il faut les compter selon le grand temps imparfait.
On voit ainsi que si le temps parfait offre trois espèces de prolations, comme il se divise en trois semi-brèves, le temps imparfait lui aussi offre deux espèces de prolations, la petite et la grande, comme il se divise en deux semi-brèves.
A noter que le grand temps imparfait se comporte comme le temps parfait moyen [11]
Fin de l'ARS NOVA de Philippe de Vitry [12]
Deo gratias.
Amen. Amen. Amen.
Notes
(du traité par les musicologues traducteurs André Gilles et Jean Maillard)
[1] Ce passage passage reproduit, un peu moins clairement, Boèce, de Arithmétique I, 32 « Demostratio quernadmodum omnis inaequalitas ab acqualitate processcrit » et de Muica II, 7 « Omnein inacqualitatem ex aequalitatc procedere ejusque demonstratio ». Le schéma explicatif qui suit devrait, pour exprimer plus clairement le processus, être construit, selon Boèce même
1 1 1 (tres unitates in uno loco)
1 2 4
1 3 9
1 4 16 etc.
[2] Le texte du Vaticanus et celui du ms Paris, BN 18514 sont ici très proches, et l'on pourrait, en faisant figurer entre crochets les leçons propres au 18514, établir le texte suivant :
« primo ponendus est tonus, deinde alius tonus, et postea semitonium, <etc....> usque ad 12 d <sequens>, quod finis dicitur <primi ordinis cliatonici generis> propter confusionem differentiarum; deinde ab <octavo> G usque ad 12 d <sequens, et ita finis est secundi ordinis propter rationem supradictam> ; deinde <incipiendo tertium ordinem diatonici generis> a <15> g usque ad 20 (19 dans le 18514) et ultra si possibilitas sit in voce. »
« Il faut d'abord poser un ton, puis un autre ton, ensuite un demi-ton, etc. jusqu'au d 12 qui suit, et que l'on appelle fin de la première succession diatonique, les états se trouvant confondus ; puis de G 8 jusqu'au d 12 qui suit, et c'est la fin de la seconde succession diatonique, de g 15 jusqu'à (ee) 20 et au-delà si le
registre est plus étendu. »
Il est certain que le texte du Vaticanus est ici très altéré, beaucoup plus que celui du ms BN 18514. Il se peut aussi que le texte du 18514 soit lui-même fautif. Mais peut-être convient-il de ne pas rejeter a priori une conception selon laquelle chaque succession diatonique serait constituée de douze signes, au lieu de correspondre à notre gamme moderne.
[3] Voyez annexe (schéma des proportions de la gamme).
[4] La musica falsa, ou ficta, est en fait de règle dans l'Ars Nova, mais elle constitue une dérogation à la succession diatonique. C'est ainsi qu'il convient d'entendre l'adjectif « irrégulière » (latin = inusitata)
[5] Cette note, telle qu'elle figure dans le ms, est incompréhensible. On devrait traduire en effet : « Il semble qu'elle doive plutôt contenir deux tons et demi qu'un ton et demi, parce que le diton, de soi, contient deux tons. Si donc on en ajoute un, il semble que cela fasse deux tons et demi (ou demi-ton). Il faut répondre en invoquant cette règle : quand, dans l'arrangement des nombres, le plus petit précède le plus grand, comme 14 - 1 devant 4 - il faut ôter une unité du plus petit. De même pour le semiditon ».
Nous rappellerons toutefois qu'il arrive à notre copiste d'écrire sans comprendre. Nous n'en sommes que plus à notre aise pour faire la remarque suivante, due aux suggestions éclairées de M. Guy Baujouan : quand on écrit les nombres en chiffres romains, on se trouve amené parfois, pour les interpréter correctement, à retrancher d'un chiffre le chiffre précédent, comme dans les groupes IV et IX. On peut supposer que le Maître aura, dans son exposé oral, cité en exemple le nombre XIV, entendu en chiffres romains, et que l'élève, sans comprendre où le maître voulait en venir, l'aura noté 14, en chiffres arabes. Le maître aura rappelé ensuite que, dans ce cas, il fallait retrancher l'unité - représentée par le petit nombre - du grand nombre qui suivait; mais, tandis qu'il songeait au V romain, l'élève écrivait « 1 ante 4 », ce qui représente sans doute un petit nombre suivi d'un plus grand, mais ne peut servir d'exemple pour la règle évoquée. Par ailleurs, « adjuncto uno » ne s'explique guère. Nous lisons plus volontiers « adjuncto dimidio ».
On notera l'intérêt que présente l'utilisation des chiffres arabes dans notre ms.[6] Cf. p. 65. lines 49-50 & note 49.
[7] Il y a désaccord dans le ms entre cette indication et la représentation correspondante. Les traits obliques 1sont en effet fréquemment utilisés par les théoriciens.
[8] Le Ms B.N. lat. 14.741 (Cf. sup.) donne seulement Deus Judex. Nous ne possédons pas d'autres indications sur ce motet. Notons seulement qu'un des versets du Psaume VII commence par Deus judex justus et f ortis et patiens. L'Abbé Ulysse Chevalier signale dans son "Repertorium hymnologicum" le motet Deus judex justus avec la référence Paris B.N. lat. 1121 f° 198 a.
[9] Ici, le Ms 14741 est muet. Coussemaker a édité "Misera": cependant la copie du Ms établie pour le Père Martini était correcte - Misera pliconia -. Bien que ce groupe soit inexplicable, la leçon "pliconia" invite à penser qu'il s'agit du motet "Mariae praeconio devotio". On trouvera précisément mention de ce motet dans le Ms Paris, B.N. lat. 11.266 f° 33 r° (Couss.; Script. I, 279) dont plusieurs passages sont fort proches de notre texte. Au f° 37 r° du même Ms, le même texte musical est repris et se poursuit au verso:
Ce motet est signalé par Eue Salomon (Scientia Artis Musicae, 1274, Gerb. Script. III, 61 b): "Qui voluerit experiri erroneum cantorem, et etiarn quasi eminentem, inducat eum ad cantandum prosam, quam edidit Dominus Clemens, Mariae praeconio". Cf. aussi Ms de Montpellier Bibi, de 1'Ecole de Médecine H 196, f° 319v et Y. Rokseth, Les Polyphonies du XIIIème siècle III, Paris 1936, p. 149, no. 283, ainsi que A. Gilles et J. Maillard, "Note sur trois motets fantômes de l'Ars Nova de Philippe de Vitry", Revue de Musicologie XXXIX (1957), p. 147.
[10] Encore qu'elle ne soit pas nommée, c'est ici de la syncope qu'il s'agit. cf.. 7378 A f 62 r G, 1.59-63 "Inveniuntur aliquotiens unice semibreves, breves ai* Iongas sequentes, que tamen eas nec augent nec minuunt, sed potius ad invicn reducuntur. Dicendum quod ponuntur 111e ut per eas recta mensura syncopetur,
secundum aliquos deberent fieri rubee", et Muris, Ars Discantus, in Couss. Scri.. III, 106.[11] Le Vaticanus parle ici du grand temps parfait: "maius tempus perfectum". On pourrait a la rigueur comprendre, ce qui n'est pas indiqué plus haut, que les minimes, comme dans le grand temps imparfait, se divisent en deux semiminimes. Toutefois, comme la minime ne se divise jamais qu'en deux semiminimes dans le système qui nous est ici proposé, on comprend mal une telle remarque. Il est beaucoup plus intéressant de constater que, dans le temps parfait moyen, comme dans le grand temps imparfait, le temps, représenté par trois semibrèves imparfaites ou deux semibrèves parfaites, a la même valeur, soit six minimes. Le ms Paris, BN 14741 vérifie cette hypothèse: "On pourrait dire que la prolation (division de la semibrève en minimes) mineure du temps parfait et la prolation majeure du temps imparfait sont identiques. Réponse: c'est vrai si l'on considère la division (division de la brève en semibrèves) et la prolation".
Soit dit aussi que le ms 14741 développe les chapitres "Dénominations des temps parfaits et imparfaits" en proposant pour chacun d'eux un exemple de motet :
Nature du temps : Titre du motet : Grand temps parfait Qui doloreux Temps parfait moyen Imperatrix anglica Petit temps parfait O Maria affectu Grand temps imparfait Gratissima virginis species Petit temps imparfait Qui aux promesses de Fortune se fie [12] Cf. aussi A. Cilles, "Contribution à un inventaire analytique des manuscrits intéressants l'Ars Nova de Philippe de Vitry", Revue Belge de Musicologie X (1956), 149-154.
...
Annexe (des traducteurs)
Tableau établi selon les données du chapitre "De operatione monochordi". Ce tableau rejoint celui de la p. 5, y compris b mol, qui n'apparaît qu'à partir des "acutae", le premier hexacorde étant par bécarre et tout entier dans les "graves".
_________FIN DE L'ARS NOVA DE PHILIPPE DE VITRY
traduit du Latin par André Gilles, Jean Maillard
_________
TELECHARGEMENTS, publication de l'ARS NOVA avec les schémas :
. texte français fichier OO .odt 120Ko
. texte français fichier .pdf 196Ko
. texte latin en 20 images .png (en cours)
ARS NOVA
app. 1320
Induction (amener à l’esprit)
J'ai décidé de rendre accessible l'Ars Nova de Philippe de Vitry (le sortir du monde confiné des musicologues spécialisés), car c'est un passage important dans notre histoire de la musique occidentale. En effet, l'Ars Nova peut être considéré comme le premier écrit théorique (qui nous est parvenu) qui s'attache à vouloir faire évoluer la musique. Dans l'appellation même « Ars Nova » = nouvel art (art nouveau), il y a la volonté : « d'innover », de désirer quelque chose de différent, de « nouveau ». Depuis 1320, l'innovation en musique (savante = qui se pense, pas celle qui se prend au sérieux) est une tradition qui se perpétue jusqu'aujourd'hui. C'est Pierre Boulez (le passionné, pas l'empereur) qui m'a communiqué l'importance de cet ouvrage qui a soutenu le mouvement de la musique sérielle (la musique sérielle qui désirait sortir la musique du joug de l'harmonie tonale en généralisant le dodécaphonisme d'Arnold Schönberg dont son principe fondateur est l'égalité contre la hiérarchie). Instaure le lien entre les polyphonistes de la pré-Renaissance (la Renaissance est un terme d'historien) aux sérialistes du XXe siècle. Il s'agissait d'épanouir la polyrythmie dans la complexité (jusqu'à la combinatoire de 12 valeurs de durée dans le phrasé musical). Ça explique aussi le non développement harmonique du sérialisme (des 3400 accords environ non utilisés par l'harmonie tonale).
L'Ars Nova, à le lire aujourd'hui, décontextualisé, est difficile d'accès, difficile à comprendre car : il manque des éléments pour comprendre. L'Ars Nova ne ressemble pas à un traité, mais plus à l'écriture de principes pour ne pas les oublier : des notes. Ce qui manque, c'est sur quoi ces principes sont fondés. Et donc, tout est interprétable.
Par exemple, la division du monocorde (le monocorde est un instrument pour se repérer. À l'époque, il n'y avait ni diapason ni métronome et la musique savante était vocale, la musique instrumentale avec le consort de violes, est apparue le siècle suivant. Pour repérer les hauteurs, on utilisait le monocorde : une seule corde tendue sur un résonateur. Pour décrire la gamme (gamma = Γ, la lettre G de l'alphabet grec), les rapports d'intervalle, Γ (s')utilise le monocorde. Et c'est ici qu'il semble y avoir une confusion de la part des musicologues : où la rencontre des mathématiques et de la musique instaure une approche contestée de la gamme présentée. Si l'on se réfère à la description des rapports (fractions x/y) décrits du point de vu du mathématicien, les intervalles résultants n'ont aucun rapport avec la division de l'octave en 12 intervalles : les rapports sur un instrument sont logarithmiques : les intervalles égaux se resserrent vers l'aigu (se remémorer les positions des frettes sur le manche de la guitare) ; alors que théoriquement et à l'écoute la division de l'octave reste égale. Il est impossible de dire si la musique de l'Ars Nova du XIVe siècle utilisait une gamme diatonique : avec « le mode majeur » tel qu'on le connait approximativement (puisque l'échelle de 12 1/2 tons a été égalisée au XXe siècle après avoir été tempérée au XVIIIe), ou pas. Reste l'approximation proportionnelle qui suffit à la musique, car elle se réfère de sonorités et non de rapports numériques.
Schéma d'interprétation mathématique de la description des intervalles dans l'Ars Nova de Philippe de Vitry sur le monocorde :
Notons que le mathématicien (mon père) ne prend pas en compte le contexte du monocorde, il applique textuellement les rapports qui sont écrit. Voici le schéma de cette description appliquée au contexte de la division de la corde :
Voici maintenant l'interprétaion des musicologues Gilbert Reaney, André Gilles et Jean Maillard du XXe siècle (1957) :
Les rapports de divisions avancés d'après Boèce au VIe siècle restent :
256/243 9/8 32/27 81/64 4/3 quarte harmonique 729/512 3/2 quinte harmonique 128/81 27/16 16/9 243/128 2/1 octave harmonique (?) fichier Scala .scl pour entendre la gamme (sur les VSTi qui considèrent Scala) : gamme Boèce de l'Ars Nova ? Ici fichier .nkp pour sampler Kontakt.
QUESTIONNEMENTS
Comment comprendre sans interpréter ce que Philippe de Vitry exprime succinctement dans son Ars Nova en 1320 ? À 1ere lecture, je ne comprends rien. Pour réaliser le lien avec notre contexte actuel (notre façon de comprendre le monde, ici par la musique) avec celui du XIVe siècle, il faut des correspondances d'équivalences. La première équivalence est la corde tendue divisible (base civilisationnelle qui traverse 25 siècles). Les 1ers intervalles de la série harmonique sont absolus : 8ve, 5te, 4te : leurs sonorités sont bien identifiées (comme + tard, la 4te+). L'introduction du 0 (zéro) date du XIe siècle en Europe (par l'Espagne, en usage en Inde depuis IIIe siècle). Le zéro est nécessaire pour exprimer le résultat des nombres rationnels de la forme : x/y (ex. 1/2 = 0,5).
Au chapitre 2 Vitry énumère les 13 intervalles connus (dont l'unisson est l'intervalle nul : 0, concept que ne connaissait pas encore Philippe de Vitry ? la place du 0 est prise par le 1)
1. unisson 1
2. octave 2
3. quinte sesquialtère 3/2
4. quarte sesquitierce 4/3
5. ton sesquioctave 9/8
6. tierce mineure (27+5) 32/27
7. tierce majeure (64+17) 81/64
8. demi-ton (243+13) 256/243
9. sixte mineure (81+47) 128/81
10. sixte majeure (32+22) 54/32
11. septième mineure (9+7) 16/9
12. septième majeure (256+230) 486/256
13. triton (512+217) 729/512Pour une gamme conjointe, nous obtenons la suite :
1. unisson 1
8. demi-ton (243+13) 256/243
5. ton sesquioctave 9/8
6. tierce mineure (27+5) 32/27
7. tierce majeure (64+17) 81/64
4. quarte sesquitierce 4/3
13. triton (512+217) 729/512
3. quinte sesquialtère 3/2
9. sixte mineure (81+47) 128/81
10. sixte majeure (32+22) 54/32
11. septième mineure (9+7) 16/9
12. septième majeure (256+230) 486/256
2. octave 2Dont la suite en cents (calculé par Scala) :
0. 1/1 0 unison, perfect prime 1. 256/243 90,225 limma, Pythagorean minor second 2. 9/8 203,91 major whole tone 3. 32/27 294,135 Pythagorean minor third 4. 81/64 407,82 Pythagorean major third 5. 4/3 498,045 perfect fourth 6. 729/512 611,73 Pythagorean tritone 7. 3/2 701,955 perfect fifth 8. 128/81 792,18 Pythagorean minor sixth 9. 27/16 905,865 Pythagorean major sixth 10. 16/9 996,09 Pythagorean minor seventh 11. 243/128 1109,775 Pythagorean major seventh 12. 2 1200 octave comparée à notre échelle égalisée usuelle
0. 1/1 0 unison, perfect prime 1. 12√2 100 equal minor second 2. (12√2)2 = 6√2 200 equal major second (whole tone) 3. (12√2)3 = 4√2 300 equal minor third 4. (12√2)4 = 3√2 400 equal major third 5. (12√2)5 500 equal fourth 6. (12√2)6 = 2√2 600 equal tritone 7. (12√2)7 700 equal fifth 8. (12√2)8 800 equal minor sixth 9. (12√2)9 900 equal major sixth 10. (12√2)10 1000 equal minor seventh 11. (12√2)11 1100 equal major seventh 12. 2 1200 octave Leonardo Fibonacci est l'une des 1ere grande influence mathématique au XIIIe siècle, dont sa série (la série de Fibonacci 1 1 2 3 5 8 13 21 34 55 89 144 etc. qui se forme en additionnant son résultat précédent et dont les rapports tendent vers le nombre d'or 1,61764...) a dû influencé Philippe de Vitry au vu de son chapitre IV « De proportionibus » (des proportions) qui propose des proportions (traduit en « rapports », mais le mot rapport fait + référence au « ratio » de fraction que de la raison d'une suite de nombre, mais bon...) par opérations pour former des séries de nombres suivants :
1. simple au double pour former la suite : 1 2 4 [8 16 32 64 128], et en ordre inverse : [128 64 32 16 8] 4 2 1
2. « sesquialtère » nombre qui s'additionne de sa moitié pour former la suite : 4 6 9 (dans le champ des durées ce sont des valeurs pointées) et 13,5 puis 20,25 puis 30,375 etc.
3. « superbipartiel » nombre qui s'additionne de ses 2/3 : 9 15 25 et 41,666... puis 69,444..., mais Vitry n'inscrit aucun nombre à virgule.
4. double et « sesquialtère » : 4 (8+2) 10 (20+5) 25
5. double et « superbipartiel » : 9 (18+6) 24 (48+16) 64À quoi servent ces suites ? est non dit, ni développé. Mais les opérations : extraction de sa moitié et de ses 2/3 et addition pour obtenir une autre valeur déduite : que ça et sans virgule. C'est à partir de cette opération que d'une proportion, il en établit deux. Du rapport x/y = z, par doublement il donne : x²/y² = z² puis le rapport des deux résultats z/z² sont les 2 rapports obtenus (pas x.x²/y.y² ou si ?) reste imprécis par manque de données.
exemple : 3/2 = 1,5 9/4 = 2,25 si l'on multiplie le premier terme par le second, on a : 3/2 . 9/4 = 27/8 = 3,375
mais dans son calcul, il trouve le « moyen » (terme) 6 :
9 4
6
3 2
Comment procède-t-il ? à part soustraire 9 à 3 et additionner 4 à 2 ? et non 9 - 2 et 3 + 4 pour 7 ?Avant le XXe siècle la dénomination de ton n'était pas le nom d'un intervalle absolu mais relatif : un ton septimal 8/7, majeur 9/8, ou mineur 10/9 : en cent, ça donne une tolérance de 50 environ (<=> 1/4 de ton) entre 180 à 230 (en cent le ton tempéré vaut 200) voir + en dehors de la considération harmonique de sa suite. Même chose pour le semiton entre 70 et 120 cent (une tolérance proportionnellement + large que pour le ton : une tolérance d'un quart de ton <=> 2x +). Pourtant Vitry considère bien le ton majeur harmonique pour ce qu'il est : 9/8 (= 1,125 ton majeur 203,910 cent. Tempéré <=> 6√2 = 1,12246 <=> 200 cents). Si Vitry identifie le ton majeur 9/8 (203,91... cents), il identifie aussi le semiton majeur : sa moitié : 9/16 ou 15/14 (119,4428 cents) de la série harmonique ? il ne l'écrit pas. S'il connaissait les rapports de la série harmonique, pourquoi en déduire d'autres par extraction de moitiés et de tiers ? Il semble que la proportion est un sens + important qu'aujourd'hui : la proportion met en rapport. Binaire (moitié) de 2 et ternaire (1/3) de 3. Aujourd'hui, les intervalles sont disposés sur un clavier, à l'époque, ils étaient chantés et le seul repère était le monochordi (sans diapason fixé).
En constituant le tableau des proportions de division de la corde tendue (du monocorde) suivant les indications de Philippe de Vitry, on obtient 24 intervalles dont la fondamentale gamma « Γ », son octave « G » (doublement) et sa quarte « g » puis « C » double octave et « c » sixte mineure « D » octave + quinte et « d » quinte, voire le « bbb » (noté 3 b superposés) qui forme une 2de majeure = le ton, rentrent, s'emboitent dans la gamma diatonique (= mode majeur) : les 16 autres intervalles ne rentrent pas dans la gamme de tons (9/8) et semitons (15/14).
Γ (corde à vide, son fondamental)
A (positionné à la 3ce majeur +~1/4 de ton du son fondamental)
B (positionné au ~5/6 de ton du son fondamental)
C (positionné à la double octave du son fondamental)
D (positionné à l'octave + quinte du son fondamental)
E (positionné à la seconde mineure + ~1/4 de ton du son fondamental)
F (positionné à l'octave + seconde majeure + ~1/3 de ton du son fondamental)
G (positionné à l'octave du son fondamental)
a
b
c
d
e
f
gPuis tons et semitons qu'il note dans la suite :
t t s t t s t t s s t t s t t s s t t alors que « notre » gamme diatonique (ou mode majeur) répète la série suivante :
t t s t t t s t t s t t t s t t s t t t s (pour/sur 3 octaves => 3 répétitions)Ce qui est intéressant, c'est que le mode majeur (gamma diatonique) est identifié par le nom de ses « notes » donné 2 siècles plus tôt par Guy d'Arezzo : ut ré mi fa sol la (sans le si). Il n'y a pas de note « si » dans la gamme de Philippe de Vitry. Où est la septième note alors ? du mode à 7 notes, heptatonique, majeur : le mode noté est à 6 notes (hexacorde = 6 cordes) et se chevauchent 7 fois dans l'étendue des 20 intervalles (les b bb et bbb sont ignoré dans la suite).
Les musicologues (Reaney, Gilles et Maillard) qui ont traduit l'Ars Nova (en 1957) semblent avoir confondu la division d'une corde avec la division équidistante d'une droite en 12 parties qui divisent l'octave et ne peut pas correspondre à la division (du mono) corde tendue ou le positionnement du doigt ou des frettes est logarithmique pour une progression d'intervalles équidistants (voir les positions des frettes sur le manche d'une guitare). Il y a aussi un doute à ce qu'entendait les musiciens de l'époque comme ton et semiton (le mot ton vient de tendu pour la corde)
Au chapitre IX Vitry parle de « propriétés musicales » qui aujourd'hui se traduit en « transpositions » et non en « altérations locales ». Le bécarre signifie la lettre « b » carrée. Le b carré dans la déduction de sa suite d'intervalles, représente approximativement 5/6e de ton et sa moitié bb carré 5/12e de ton qui respectivement approximativement en cent donne 166,6... et 83,3... Mais en même temps de b carré place l'hexacorde 1 ton au-dessus de A a et aa et le b mol 1 semiton au-dessus de a et aa (l'état « naturel » ne bouge rien).
...
Mais l'apport majeur de l'Ars Nova n'est pas la gamme, mais LA POLYPHONIE. Plusieurs voix indépendantes (voix féminine haute et basse, voix masculine haute et basse) qui chantent à des vitesses différentes, commençant avec le 3 pour 2 : une mesure ternaire en même temps qu'une mesure binaire (imparfaite).
_
Note et références
Par les publications libres du centrebombe (les éditions anonymes électriques gratuites des mises en réseau du centrebombe : EA)Il y a des traités théoriques de la musique qui sont importants (des charnières essentielles) pour comprendre l'évolution historique de la musique savante (réfléchie) en Occident. Peu de personnes les lisent par manque d'accessibilité, comme le traité de l'Ars Nova Musicae de Philippe de Vitry (~1320) toujours inaccessible au lecteur, enfermé ou perdu à la Bibliothèque Nationale de France, BnF*) (* Il y aurait une traduction, sans doute celle à laquelle Pierre Boulez devait faire référence pour alimenter la « théorie sérielle » : Philippi de Vitriaco Ars nova, éd. et trad. fr. Gilbert Reaney, André Gilles et Jean Maillard, Roma, American Institute of Musicology (Corpus scriptorum de musica, 8), 1964, 93 pages, réimpression de l'édition de 1956 en plus de nombreux articles relatifs à l'Ars nova. Rapporté par Arlima (archives de littérature du moyen-âge : http://www.arlima.net/mp/philippe_de_vitry.html. Une autre en anglais de Leon Plantinga en 1961. Jean-Marc Warszawski à http://www.musicologie.org/Biographies/p/philippe_de_vitry.html publie un extrait dont il ne site pas la source).
Catherine Ann Lloyd ARS ANTIQUA - ARS NOVA (King's College London, April 2002)
Philippe de Vitry's Ars Nova, trad. Leon Plantinga, Music Theory 5 (november 1961),
Le manuscrit original (sous la référence C 222, f. 3-7 ?) que détenait la Bibliothèque municipale de Strasbourg a été détruit dans le bombardement de la bibliothèque le 24 août 1870 (! Arlima). D'autres copies doivent exister, car il y a plusieurs traductions introuvables et citées : la première en 1890 (20 ans après la destruction du manuscrit de Strasbourg), la seconde d'André Gilles, Jean Maillard et Gilbert Reaney (musicologue anglais) en 1957, et une troisième en 1961 par le musicologue américain Leon Plantinga du département de Music de l'université de Yale de 1963 à 2005.
Reste une copie italienne du manuscrit dont la musicologue Karen Desmond rapporte : "This key music theory text within the fourteenth-century Ars nova tradition is found in three manuscript sources of Italian provenance dating from the fourteenth and fifteenth-centuries: in a manuscript copied by G. Frater de Anglia in Pavia in 1391, and now preserved in the Newberry Library in Chicago (Ms. 54.1, ff. 52v-56v, hereafter Cn); in a manuscript of Italian and Catalan origin dating from the early fifteenth century, Seville, Biblioteca Capitular y Colombina, Ms. 5-2-25, ff. 63r-64v (hereafter Sc); and a late fifteenth-century paper manuscript of Italian origin, Siena, Biblioteca comunale, Ms. L.V.30, ff. 129r-129v (hereafter Su)." http://www.arsmusicae.org/wordpress/blog/category/medieval-music-theory dont la publication de l'Omni desideranti notitiam est lisible ici : http://www.arsmusicae.org/
Dr. Karen Desmond
Banting Fellow, Schulich School of Music, McGill University (2014-2016)
NEH Fellow, Jan-Dec 2014
Email: karen.desmond@nyu.eduhttp://www.arsmusicae.org/wordpress/blog/category/medieval-music-theory/
http://www.arsmusicae.org/
http://www.arsmusicae.org/chicago.xml
http://www.arsmusicae.org/seville.xml
http://www.arsmusicae.org/files.htmlSite la référence :
Philippi de Vitriaco Ars nova. Edited by Gilbert Reaney, André Gilles and Jean Maillard. Vol. 8, Corpus scriptorum de musica. [Rome] : American Institute of Musicology, 1964.Je détiens une copie de la traduction de 1957, la seconde révision de 1964 republiée en Allemagne en 1986 et trouvée aux Etats-Unis !
Ce que détient la BnF est la traduction du musicologue britannique Gilbert Reaney avec les français André Gilles et Jean Maillard, de 1956-57 (semble-t-il) :
Philippe de Vitry. Ars Nova. [French translation] André Gilles, Jean Maillard (fr), Gilbert Reaney (engl)
Description matérielle : P. 12-30, In-4°, musique
Description : Note : Dans : Musica disciplina, Rome, 1957, XI
Édition : Rome : [s.n.] , 1957
Traducteur : Gilbert Reaney (1924-2008)
Auteur du texte : Philippe de Vitry (1291-1361)Ars nova..., a Gilbert Reaney, André Gilles et Jean Maillard, edita
Description matérielle : P. 13-33, In-4°
Description : Note : Dans : Musica disciplina, Rome, 1956, X
Édition : Rome : [s.n.] , 1956
Auteur du texte : Philippe de Vitry (1291-1361)
Éditeur scientifique : Gilbert Reaney (1924-2008)Philippi de Vitriaco. Ars nova [textes latin et français, suivi de : Paris, Bibliothèque nationale, lat. 7378 A, texte latin et trad. française en regard ; Londres, British Museum, Add. 21455 ; Anonyme III de Coussemaker (Paris, Bibliothèque nationale, lat. 15128)] , a Gilbert Reaney, André Gilles et Jean Maillard, edita
Description matérielle : In-8° (24,5 cm), 93 p., musique
Édition : [S.l.] : America institute of musicology , 1964
Auteur du texte : Philippe de Vitry (1291-1361)
Éditeur scientifique : Gilbert Reaney (1924-2008)Philippi de Vitriaco. Ars nova [textes latin et français, suivi de : Paris, Bibliothèque nationale, lat. 7378 A, texte latin et trad. française en regard ; Londres, British Museum, Add. 21455 ; Anonyme III de Coussemaker (Paris, Bibliothèque nationale, lat. 15128)], a Gilbert Reaney, André Gilles et Jean Maillard, edita
Description matérielle : In-8° (24,5 cm), 93 p., musique
Édition : [S.l.] : American institute of musicology , 1964
Auteur du texte : Philippe de Vitry (1291-1361)
Éditeur scientifique : Gilbert Reaney (1924-2008)La Bibliothèque de l’Institut de Recherche et d’Histoire des Textes (CNRS/IRHT UPR 841)
40, Avenue d'Iéna
75116 PARIS
France
01 44 43 91 12
bibliotheque-iena@irht.cnrs.fr
http://bibliotheque.irht.cnrs.fr/pmb/opac_css/index.php?lvl=section_see&id=29&location=9&page=10&nbr_lignes=1345&dcote=&lcote=3&nc=&main=&ssub=&plettreaut=
avance que :
Titre : Ars musicae mensurabilis secundum Franconem :
mss.
Paris, Bibl. nat., lat. 15129 ;
Uppsala, Universiteitsbibl., C. 55 Anonymus ; ediderunt Gilbertus Reaney ; et Andreas Gilles.
Type de document : texte imprimé
Auteurs : André Gilles, Editeur scientifique ; Gilbert Reaney, Editeur scientifique
Editeur : Rome : American Institute of Musicology
Année de publication : 1971
Collection : Corpus Scriptorum de Musica num. 15
Importance : 74 p
Présentation : mus
Format : 24 cm
Note générale : Ce texte est précédé de : Petrus Picardus, Ars motettorum compilata breviter ; et suivi de : Anonymus, Compendium musicae mensurabilis artis antiquae.
Bibliogr.
Langues : Anglais (eng)Titre : Ars Nova : Philippi de Vitriaco ; a Gilbert Reaney ; André Gilles ; et Jean Maillard edita.
Type de document : texte imprimé
Auteurs : Philippe de Vitry ; Jean Maillard, Editeur scientifique ; André Gilles, Editeur scientifique ; Gilbert Reaney, Editeur scientifique
Editeur : Rome : American Institute of Musicology
Année de publication : 1964
Collection : Corpus Scriptorum de Musica num. 8
Importance : 94 p
Format : 25 cm
Langues : Anglais (eng)1 exemplaire existe à Orléans section musicologie cote 12 et MUS. 8° W 74 (8) et est exclu du prêt
l'ARS NOVA est lisible en latin là :
http://www.chmtl.indiana.edu/tml/14th/VITANV_MBAVB307.html
http://www.chmtl.indiana.edu/tml/14th/14TH_INDEX.html
http://www.chmtl.indiana.edu/tml/14th/VITARNO_TEXT.htmlIndex of /tml/14th (textes sur la musique du XIVe siècle)
http://www.chmtl.indiana.edu/tml/14th/THESAURUS MUSICARUM LATINARUM
Jacobs School of Music
Indiana University
Bloomington, IN 47405
http://www.chmtl.indiana.edu
Courrier / discussion :
30 mai 2016
de Gui Bryennes[lettre de Gui Bryennes au format pdf 126KO]
DISCUSSION (pour engager l'échange avec d'autres) :
Merci Gui pour votre intérêt à la musique. La théorie établit la fondation qui ajuste les instruments de musique à jouer tels rapports (intervalles) de vitesses (hauteurs) au détriment d'une autre, tous dépendants d'un système de correspondances qui crée une « certaine » cohérence dans la résolution des coïncidences. La division de l'octave en tant qu'intervalle majeur, s'explique par sa position 1re dans la série harmonique postulée par Pythagore (avec la quinte et la quarte à sa suite). L'intervalle d'octave (le double 2 ou la moitié 1/2 du double) correspond à l'effet de l'attraction terrestre. La résolution (le finale) se termine par/dans lui : la « cadence parfaite » (sic) de l'harmonie tonale. Il s'agit bien de tourner en rond dans l'horloge scalaire (transpositions) de 12 horaires-1/2-tons pour revenir à la tonique appuyée de l'octave pour achever la musique.
Gui - si Γ est le son fondamental, G l'octave, comment g est-il la 4te par exemple ?
Mathius - le 1/4 de Γ (1) est la valeur de « g » = 0,25. En effet, la moitié d'une octave (dans le domaine de l'algèbre linéaire) est une quarte augmentée : 4t+. Mais sur une corde les rapports ne sont pas équidistants ni linéaires, mais logarithmiques : au quart de la corde correspond le 4e harmonique de la quarte et donc la quarte elle-même. C'est ce qui a confondu le calcul des musicologues, car Vitry compte les proportions de la corde vibrante et non les rapports numériques dans la linéarité.
G - je ne comprends pas non plus les fractions de ton qui apparaissent dans cette correspondance (par exemple cc <=> 3ce m + ~1/4 ton).
M - cc est positionné à la moitié de c la moitié de C (toujours dans les proportions logarithmiques de la division de la corde) la proportion logarithmique 0,1875 correspond à une 3ce mineure + approximativement 1/4 de ton.
G - Γ est placé à droite correspondant à la corde à vide et où donc les longueurs de corde vibrante sont à gauche des frettes,
M - non, dans ce cas le monocorde serait la tête en bas. Dans le schéma, la corde vibrante est à droite et les frettes sont à gauche. Un droitier utilise sa main droite pour faire vibrer la corde et sa main gauche pour la raccourcir à partir des frettes positionnées sur le manche à gauche, en étant soi-même positionné à droite de l'instrument. Pour les gauchers c'est le contraire : à gauche de l'instrument, la main gauche fait vibrer et la main droite raccourcit. Dans les 2 cas ça ne change pas la disposition de l'instrument. Dans le grand schéma, je considère les positions (de tons) qui raccourcissent la corde vibrante « à vide » à gauche (les frettes à gauche).
G - A ne doit pas être placé au 1/3 de D (donc à l'aigu de D) mais de l'autre côté à 4/3 de D (c-à-d au grave de D).
M - A est bien positionné au grave de D dans l'espace logarithmique de la corde.
G - le B (notre 'si bécarre') doit être placé à 4/3 de E (au grave de E).
M - pareil, B est bien positionné au grave de D dans l'espace logarithmique de la corde.
G - Dans le schéma à main levée qui figure avant il y a aussi une erreur de placement de A, B, E et de leurs octaves supérieures mais ce mauvais placement n'est pas le même que celui du grand schéma.
M - le schéma à main levée montre comment un mathématicien non musicien comprend le positionnement des proportions par rapport à la description de Philippe de Vitry. Je l'ai publié pour ça, à montrer que tout théoricien non musicien se perd dans le domaine qu'il ne pratique pas : ce qui a été le cas des savants qui ont faussement traduit (était-ce vraiment leur intention, je ne pense pas) la théorie musicale Hellène. Je pense aussi à Euler éminent mathématicien qui pestait contre Bach du fait qu'il ait introduit la transposition sur les 12 tonalités de l'échelle (unique) et forcé le tempérament (la tempérance = la tolérance) pour ça. La figuration harmonique du son 1 2 3 4 5 6 ... est un possible qui n'est pas absolu, voire une exception.
Je pense que les musicologues sont allés un peu vite, tels les savants au début de notre ère à vouloir « traduire » la théorie musicale Hellène de la Grèce Antique dont les fragments d'Aristoxène nous donnent un vague aperçu de la richesse théorique musicale perdue, en échange d'une dominante majeure (monomodale fidèle au monothéisme) réduisant la multiplicité à l'unicité en accord avec l'idéologie chrétienne patriarcale encore et toujours en usage aujourd'hui. Après 2000 ans, je pense qu'il est important de changer de route (de figuration idéologique du monde = de mythe) en réintroduisant la diversité. Sans elle, la musique souffre. Ma théorie des amas des champs scalaires nonoctaviants propose une porte de sortie harmonique et de synthèse.
G - Si Γ correspond à 12, alors le G est à la moitié (donc à 6) et g à la moitié de la moitié (à 3), le C est à 3 parties sur 4 de la longueur de G donc sur 9, le D est à 2 parties sur 3 de la longueur de G (donc sur 8), d à la moitié de la longueur de D (sur 4) et dd à la moitié de la moitié (sur 2) (pour ces derniers le schéma manque de précision)
M - Vous calculez dans le domaine linéaire et non logarithmique. Mais suivant votre description nous avons :Dans les 2 domaines lin éaire et logarithmique (exponentielle inverse) l'origine et le 1er rapport 1/2 correspondent ensuite, ils s'écartent.
Γ
G
g
C
D
d
ddunisson
octave
triton
6te M
6te m
3ce M
2de M12
6
3
9
8
4
2OK
OK
NON
NON
NON
NON
NONG - Le b (b rond = notre 'si b') correspond au Moyen-Âge et depuis les Grecs à la corde trite du tétracorde synemmenon.
M - je ne suis pas sûr de la correspondance « corde titre » avec le sib de notre échelle égalisée de 12 tons divisant l'octave (rapport 2) d'aujourd'hui. Le sib correspond à une position alors que la corde titre règle sa tension par une proportion = méthode d'accordage. Le diapason (pas l'octave mais l'accordeur à la fréquence fixe aujourd'hui à 440Hz = la3) est apparu au XIXe siècle. Ou pour être + simple dans le champ du temps : à une date ne correspond pas une durée. Notre sib d'aujourd'hui ne correspond en rien au sib d'autrefois à peine existant.
G - Γ, A, B, C, D, E, F, G, a, b mol, b carré, c, d, e, f, g, aa, bb mol, bb carré, cc,... qui est bien diatonique, construite sur un sol grave.
M - le diatonisme est une forme ou forme un ensemble modal qui avec le chromatisme et l'enharmonique classait les 3 types de modes des modes possibles (compréhension selon la description sommaire d'Aristoxène). Le mode hexatonique proposé par Vitry : ton, ton, semiton, ton, ton, semiton est en effet diatonique mais n'est pas le mode majeur heptatonique : ton, ton, semiton, ton, ton, ton semiton (équivalent au mode Dhira Shankarābharanam en Inde). En effet le 7e ton arrive + tard. le Si bémol ou bécarre innommé par Guy d'Arezzo 2 siècles avant ni Vitry 2 siècles après.
Les confusions inextricables de la théorie musicale se sont ajoutées 1. par mécompréhension des musiciens, 2. par mécompréhension des théoriciens mathématiciens non-musiciens et 3. par le désir religieux (politique) du christianisme dominant d'unifier la diversité dans l'unicité dans un seul mode majeur avec un mineur (qui en réalité sont 3) attribué à la « triste » (sic) féminité ! L'unicité est une régression de l'intelligence pour une expansion de l'agressivité : ça a réussi, aujourd'hui notre civilisation domine le monde par sa médiocrité.
Pour stopper la confusion entre : échelle, mode et gamme, voici une proposition : L'échelle est composée d'un même intervalle (qui se répète infiniment), le mode est composé au moins de 2 différents intervalles, et la gamme est la transdisposition du mode aux différents degrés d'une échelle (la même ou et d'autres) sans que les proportions (mais pas les distances) du mode changent, sinon il mute en autre chose (perd son identifiabilité). L'Occident post-christique a rejeté l'ensemble des modes enharmoniques des Hellènes, qui a été récupéré par les cultures proche-orientales (qui ont rejeté le diatonique et le chromatique), pour ne garder qu'un seul mode de l'ensemble diatonique et chromatique. Remarquons que la division exacte de l'octave, où par exemple un sib = la#, est propre au XXe siècle. Debussy disait à propos de l'échelle de 12 1/2 tons qu'en réalité à l'usage instrumental il considérait 24 tons où sib ≠ la#. La régression systématique de la musique dans l'égalitarisme numérique a été progressive et s'est réalisée récemment à partir du moment quand on a réalisé l'égalisation de la tempérance (= l'intolérance de la tolérance) à travers l’exactitude de l’Ordinateur et considéré la musique comme un « assemblage de sons », c'est à ce moment que la musique à partir des années 80 du XXe siècle a perdu sa vie et où toute évolution de l'intelligence semble avoir été autobannie dans la culture de l'autocensure occidentale. Les champs scalaires nonoctaviants deviennent dans ce cas d'urgence : un remède.
Quelle histoire !
Pour en revenir à l'Ars Nova à 1320, le manque d'information en rapport avec le contexte musical de l'époque qu'il lui paraissait inutile de préciser, car Philippe de Vitry ne pensait absolument pas à la postérité de son écrit 696 années + tard, auquel cas, il aurait précisé le contexte, ce qui n'est pas le cas. Le manuel ressemble + à des notes fondamentales à ne pas oublier pour structurer son enseignement oral, qu'à un traité suffisant à lui-même (à étudier dans la solitude de sa chambre d'étudiant).
Reste qu'à interpréter pour comprendre ce qui est donné, comme les partitions d'en temps réactualisées au contexte contemporain différent d'alors. Ou pas. L'essentiel, est d'ouvrir son présent (avec ce qui reste).Merci pour votre intérêt :) les personnes passionnées sont rares :(
Mathius Shadow-Sky
2 juin 2016
de Gui BryennesGui Bryennes - Si je comprends bien donc il faut lire le grand schéma en prenant les repères de gauche à droite comme allant du grave vers l'aigu. Est-ce bien cela ? (Peut-être que j'ai inconsciemment pris les traits continus horizontaux comme des longueurs de corde vibrante auquel cas on aurait G = le plus long = le plus grave).
mathius shadow-sky - OUI
G - Autrement dit, les repères successifs pris dans le grand schéma de gauche à droite : bb, b, ee, B, aa, e,... ,... G, F, D, C, G donnent l'échelle des sons du grave à l'aigu.
m - OUI
G - Dans ce cas, la disposition que je mettais : G, A, B, C, D, E, F, G, a, b rond, b carré, c, d, e, f, g, aa, bb rond, bb carré, cc, ... comme allant du grave à l'aigu à partir d'un sol grave est incorrecte. Confirmez-vous cela ?
m - OUI, en effet, cette suite n'est pas sur le monocorde une suite de hauteurs conjointes. Dans le contexte du monocorde votre suite commence à l'aigu G à l'octave de Γ (corde à vide) puis A à une tierce majeure +~1/4 de ton de Γ, puis B à 5/6e de ton de Γ, etc. Si vous avez une guitare ou mieux un violon, vous pouvez le vérifier instantanément.
Les glissements de sens ou l'appropriation d'un mot pour un autre sens comme la lettre grecque Gamma qui prend le sens actuel de gamme (éventail conjoint de différences quasi similaires ou similarisées) ou comme la signification du b carré de Vitry transformé en bécarre aujourd'hui, ou le b rond en bémol d'aujourd'hui : une localisation contre une fonction. Le sens des mots change par rapport à un contexte. Et c'est cette spécificité fondatrice qui nous échappe. Par exemple quand le mot tuer (de tuteur) a pris la place d'occire, c'était pour désigner une façon déloyale de tuer : par surprise (d'abord par étouffement). Ces musiques d'antan pourtant écrites ne seront jamais que re-interprétées au contexte présent : re-contextualisées (en fonction de nos manques fabulés). La difficulté de percevoir, voire de comprendre les autres contextes (géographiques et historiques) est difficile pour ne pas dire impossible du fait déjà de notre position inextricable dans notre propre contexte. Je pense à ces (ethno) musicologues émergés du colonialisme qui « notaient » dans le système tonal les musiques des « sauvages » (sic) ; ce encore jusqu'aujourd'hui (bien que John Blacking l'ait dénoncé en renversant l'ethnomusicologie sur nous-mêmes occidentaux).
G - Je n'ai pas lu le reste de vos pages autant que je l'aurais souhaité mais j'aimerais bien en saisir la philosophie générale. Plus qu'une théorie qui aurait pour vocation de décrire l'existant ou les règles du permis/interdit (la théorie académique, tonale, basée en grande partie sur des hiérarchies, sur une dynamique consonant/dissonant) vous souhaitez construire une « théorie » générative qui produise des échelles puis des modes « en marge » ou même « en dehors » du cadre consonance/dissonance. D'où l'exploration des espaces générés par la relation x√y.
C'est donc une perspective artistique, créative.
On crée un nouvel alphabet, un nouveau vocabulaire.
La théorie crée (?) propose (?). Le musicien choisit.
Comment s'exerce l'arbitrage du musicien ? quel discernement ? Quelles échelles « valent » plus que les autres ?
Et quelle musique ? Nouvel alphabet/vocabulaire/grammaire ? Mais quel langage ? Un chant sur un accompagnement ? (Une forme sur un fond ?) Des phrases ? pas de phrases ? Un jeu de couleurs harmoniques, des agrégats ? Un fond sans formes, ou les 2 qui se fondent.
Désolé de mes questions si elles ne font pas sens. Le point principal est de savoir comment on peut s'orienter dans la profusion du x√y. Comment on choisit. En effet pour moi le x√y couvre le monde entier des possibles.
salutations,
FraCasparism - Merci FraCasparis de me poser ces questions. La théorie des amas des champs scalaires nonoctaviants (gna gna gna = ça prend le nom que ça veut) est un épanouissement logique de l'unique vers le multiple. Le contentement d'une seule échelle revient à nier ce qui existe ici et ailleurs au-delà de la « voute » céleste du système solaire. Aujourd'hui nous estimons des Plurivers possibles, alors que la théorie musicale stationne au stade de l'attraction newtonienne. N'est pas vraiment un argument, juste un comparatif qui montre la régression ou le stationnement de l'esprit musical dominant (qui détient les moyens de réalisation). L'expérience qui au début m'a marqué était que différentes échelles en dehors de l'horloge de nos 12 1/2 tons sonnaient faussent de la MÊME manière, alors que le calcul et la forme des instruments manifestaient le contraire (tubes, cordes, sinus électroniques). La culture se construit de l'habitude, mais la musique (et les arts) tarit de l'habitude. C'est en ça que notre tradition occidentale notre histoire musicale savante renouvelle son système en permanence. Ce qui est curieux, c'est la résistance aujourd'hui acharnée au changement, enracinée dans l'idée de l'ordre représenté par le pouvoir politique hiérarchique de la fonction publique (l'administration de l'ordre) depuis le XXe siècle. Au XXIe, la haine de la différence fait de l'avant-garde des terroristes qui terrorisent les terrorisés (je me suis fait agressé après mes concerts : coups et insultes disant que jouait la musique du diable ! si si !).
Ma première musique écrite avec l'idée de s'échapper intentionnellement du cercle (vicieux) des 12 1/2 tons était Ourdission http://centrebombe.org/livre/1982a.html en 1982 avec son échelle nonoctaviante noncyclique de 41 tons destinés à la flûte traversière (il fallait libérer la turbulence de la mort). Après : Iannis Xenakis à la recherche d'autres modes (théorie des cribles) de métaboles, Ivan Wyschnegradsky sur la micro-ton-alité de ses « espaces nonoctaviants » (évitant l'octave), Harry Partch sur 13 autres divisions de l'octave et John Chowning réalisant la synthèse numérique par modulation de fréquence inharmonique, il fallait une théorie qui puisse à la fois réunir toutes ces explorations isolées (y compris la théorie tonale) et à la fois élargir le champ d'action pour sa composition musicale. Tout en effaçant la frontière entre agrégat de fréquences (harmonie élargie) et synthèse sonore.
« On ne peut pas convaincre (ça ne sert à rien que de faire souffrir) qui que soit, de quoi que ce soit de quelque chose que sa conscience n'est pas prête à comprendre (si sa conscience refuse) » forme la culture et le contexte de vie des évidences pour former les chréodes. Un humain se contente toute sa vie de ce qu'il a appris, s'ouvrir à l'inconnu et reconnaître que l'apprentissage reconnu est insuffisant positionne l'autorité du savoir dans l'incertitude qui est un état contraire à la domination de soi (surtout des autres) : en fait, c'est le contraire, car nous faisons la différence entre un esprit ouvert et celui fermé. La théorie des champs généralisés est une théorie de l'envergure qui s'étend au-delà des limites du visible et de l'audible conditionnée. Le son est le résultat inanimé enregistré (un signal illusoire de contrôle) de champs vibratoires en mouvements constants. J'ai expérimenté cet état de fait avec la musique « Il m'est impossible de donner un titre à ce phénomène, car... » en 1983 http://centrebombe.org/livre/1983b.html.
La théorie des champs scalaires vibrants dévoile un très grand nombre de possible et agit comme un système non systémique de localisation qui dépend de sa localisation culturelle et de son intention : mesure équidistante similaire pour localiser et jouer la différence. Le nonoctaviant est nécessaire pour s'extraire de la boucle répétitive de l'horloge unique de l'attraction octaviante. Il s'agit maintenant d'élaborer des musiques multihoraires qui ne s'arrêtent pas sur la dualité morale : consonant/dissonant = permis/interdit = faux/juste = obéissance/désobéissance = récompense/punition = rejet/intégration (qui crée des peines inutiles), mais bien d'aller « voir » ailleurs.
Le vocabulaire reste le même : le vibratoire qui sort de l'idéologie du son. C'est la grammaire qui se développe (notre état d'esprit à générer un amas d'opérations de transformations). Les champs sont encore vierges et il y a un travail « hors temps » en amont comme Xenakis nous l'a enseigné avant de s'atteler à la composition ou réaliser en même temps dans le contexte voulu : car ça influe ça, etc. Cette nouvelle théorie (il n'y en a pas d'autres) favorise la diversité. Le musicien va ouvrir ses oreilles pour identifier des sonorités et non plus juger entre la fausse note et la note juste qui est l’handicape de la fermeture d'esprit : obéir aux règles au lieu de les inventer au fur et à mesure du jeu. Idée que j'ai commencé à développer en 1980 avec Ludus Musicae Temporarium pour ensemble de lampes archisoniques (à base de lampe à ressorts) où le jeu développe la forme musicale. http://centrebombe.org/livre/1980.b.html
Parmi mes enregistrements récents avec les échelles nonoctaviantes en harmonie elles s'entendent dans les disques LES FANTÔMES DE L'EPHEMERÔDE album réalisé en 2014 puis le concert avec L'EPHEMERÔDE CARDE DES CHRÔNES live in Krakow sur le pianomorphe = clavier en métamorphose sonique (il y a aussi la vidéo du concert ici : http://www.ustream.tv/recorded/55713405) le tout téléchargeable et audible ici : http://centrebombe.org/myster_shadow-sky_discography.html. Depuis 1982 il y en a un peu partout. Certains retours que j'ai reçus de musiciens utilisant ces échelles (pour ceux qui parlent) sont : « on peut jouer n'importe où (sur la touche du manche du violoncelle) je n'arrive pas à obtenir une fausse note ! » (un des solistes du Voyage au bout du possible de l'homme en 2012) ; « j'ai réussi, harmoniquement à intégrer des sons dissonants que je n'arrivais pas à intégrer avec l'échelle des 12 1/2 tons ». Le choix du musicien s'opère en fonction de ce dont il a besoin : octaviante à micro-intervalle ou macro-intervalle (tout le champ du + petit au + grand est habité) proche octaviante, nonoctaviante, cyclique, noncyclique, quasicyclique ; ou un assemblement pour des constructions modales (d'un mode par échelle jusqu'à plusieurs modes formés de plusieurs échelles) en considérant leurs métamorphoses temporelles où l'identité du mode se perd dans un autre ou dans l'autre sens, où elle ne se perd pas dans sa transposition (opération tonale introduite par Bach : une belle opération qui n'a pas à être niée).
Aucune valeur n'est présupposée ni imposée dans l'esprit des champs scalaires vibrants, la valeur est une notion obsolète dans la composition musicale, car le compositeur rencontre + des problèmes à résoudre qu'à valoriser tel au détriment d'un tel ou d'autres tels, sinon il applique des stéréotypes (j'aime ça, j'aime pas ça). La valorisation est réalisée par l'auditeur qui perçoit ses préférences (conditionnées ou pas) en fonction de là où il se sent bien. Et ça, avec toutes les musiques. Pour la musique tonale, les compositeurs ont perpétuellement recherché des échappatoires à la domination figée de l'harmonie des cadences (sens du mot parallèle de l'allure à une attitude imposée et figée dans la chute avec 4 possibilités : parfaite, rompue, demi, plagale) : de « cadenza » = conclusion ET rythme (des rameurs synchronisés), les musicologues harmonistes (de l'ordre en force) retiennent la chute = « cadere » (cadavre = mort, et choir : le choeur choit) qui dans l'autre sens reste en suspens (en mort-vivant ?) l'accord continu immobile (aujourd'hui : « drone » qui s'enrichit en s'ouvrant à la complexité du noise) : que va-t-il se passer ? tin tinininin ! Ouf ! résolution dans la chute, dans la fin, la délivrance de la peine par la mort (étrange ce sens du soulagement dans le suicide provoqué et à la fois interdit par l'Eglise). La hiérarchie de l'harmonie tonale est justifiée par la chute (et une fois par terre, on ne se relève plus : c'est fini = cadavere) : V-I, IV-I, n-V, V-n (+ variantes). La Terre tonique tonale tendue, la terre corde tendue pythagoricienne 2 = Ier degré puis 3/2 = Ve degré dominant puis 4/3 = IVe degré sous-dominant qui vibre sa base à redescendre les marches harmoniques de la série des entiers naturels (pas relatifs de l'ensemble Z) est une vision limitée qui s'est figée complètement dans l'égalité numérique des ordinateurs qui a perdu sa tempérance (= sa tolérance). Comme pour Bach au XVIIIe, il fallait sortir du piège, s'évader de l'enfermement : la solution ? Multiplier les échelles (equal scales) pour opérer des métaboles des unes aux autres : les champs sont ouverts et libre d'accès.
Le glissement de sens du mot harmonie de : mettre ensemble à : ordonner de manière à satisfaire (son intolérance : sa morale) montre à quel point la société humaine occidentale se cristallise (se durcit) dans la croyance où l'incroyable, l'incrédible (crédit bancaire refusé) va jusqu'à faire souffrir. Quelle importance de croire ou pas ? L'obstination agressive des partisans de la tonalité réagissant par l'attaque en personnes blessées (que personne n'attaque) qui par l'existence du différent se sentent agressées (en insécurité => racisme offensif envers les étrangers (pauvres) femmes (faibles) artistes et le reste) est le résultat d'un symptôme de malêtre. Les attaques au XXIe siècle contre l'atonalisme, technique d'écriture historiquement obsolète qui date du début du XXe siècle, sont inquiétantes (nous sommes soucieux de ce que souffrent ces attaquants qui pour attaquer doivent être en mauvaise santé).
8 juin 2016
de Gui BryennesGui Bryennes FraCasparis - 1. Malheureusement pas en ce moment le moyen d'écouter d'exemples musicaux. Déjà qqes réflexions qui me viennent à la lecture de votre réponse mais j'attendrai une écoute pour (me) les formuler. J'ai donc laissé cela pour l'instant. Merci en tout cas beaucoup pour ces commentaires qui me donnent quelques pistes.
2. Pour le reste, je ne peux plus vous suivre. J'ai "rectifié ma vision" et donc lu le schéma en mettant le "sillet" à gauche, le "chevalet" à droite et donc les longueurs de corde vibrante à droite des frettes (donc bien "en droitier") et j'aboutis à des contradictions insurmontables :
a. sur un manche de guitare, luth ou viole le resserrement des frettes s'effectue vers l'aigu, qui est à gauche sur le schéma. Les portions de corde vibrante devraient normalement être à gauche des frettes dans ce cas. (On s'attendrait par exemple à retourner le schéma pour le voir comme un manche fretté, d'autant que la représentation respecte l'écartement des repères donné par les valeurs de proportions calculées d'après Vitry.)
b. dans les textes du M-Â, où des lettres désignent les hauteurs de son, les majuscules sont utilisées pour le grave, les minuscules pour l'aigu, les minuscules redoublées pour le "sur-aigu" avec le principe que 'aa' désigne l'octave supérieure de 'a', qui est lui-même l'octave supérieurs de 'A',... Vitry ne contredit pas cet usage : "Ceux de ces signes qui vont de Γ à G sont dits graves parce qu'ils traduisent une sonorité grave..." (Istorum signorum [Gamma] ad G dicuntur graves, quia gravem cantum reddunt,...)
c. les schémas qui figurent dans la traduction montrent bien une échelle Γ,A,B,C,D,E,... allant du grave à l'aigu avec, placées à côté, les syllabes de solmisation ut-ré-mi-fa-sol-la (du grave à l'aigu)
Rien de cela ne concorde avec le sens de lecture que vous m'avez indiqué en dernier qui était du grave à l'aigu de gauche à droite (bb, b, ee, B, aa, e,...). Là je ne peux plus du tout rejoindre votre interprétation de cette division de monocorde. Sans compter que les intervalles résultants ne forment pas un système aisé à utiliser.
3. Beaucoup de choses très intéressantes dans les pages que j'ai pu lire et aussi vos réponses précédentes. Je pense à des idées, éclairages, perspectives,... (rien que sur l'interprétation nécessaire des textes mais tout le reste aussi). Mais pas le loisir de les reporter ici.
salutations,
FraCasparis
qui cherche toujours la concorde dans les divisions de monocordemathius shadow-sky - Vous avez raison Gui, c'est incohérent, et c'est bien ça que j'ai voulu montrer par la publication de l'Ars Nova. Car selon l'essai de compréhension hors contexte de l'Ars Nova du XIVe siècle par les musicologues du XXe siècle, la même adaptation (variation, interprétation) est réalisée exactement comme les moines chrétiens qui « traduisent » la théorie musicale de la Grèce Antique (Hellène) pour « l'adapter » au chant grégorien. Bien que l'idéologie de la musique cléricale du chant d'Église n'a rien « à voir » avec la musique des Hellènes. Mais le besoin d'assise, de fondation pour justifier son acte à ce qu'il soit accepté et reconnu par les autres, passe par cette « filiation » traditionnelle (comme ma théorie des champs scalaires nonoctaviants se justifie des recherches de Wyschnegradsky, Xenakis, Marie, Partch, Chowning pour être admise et reconnu « d'utilité publique ». Même coutume dans les sciences). Bien qu'au fond, on n'a pas besoin de ça.
Avec la description de Vitry nous chutons dans l'incohérence bien que la Γ fut déjà fixée par Boèce au VIe siècle et dont Vitry s'inspire (De institutione musica que je pense republier et questionner au centrebombe, un ouvrage beaucoup + fournit).
256/243
9/8
32/27
81/64
4/3
729/512
3/2
128/81
27/16
16/9
243/128
2/1Pourtant la concordance est tout à fait réalisable en fonction de la position des frettes du monocorde (logarithmique) et la théorie des rapports linéaires qui définissent le « mode majeur ». Il suffit de connaître la longueur exacte de la corde vibrante du monocorde pour calculer les positions exactes du mode posé dans ses rapports par Boèce.
Si la corde mesure 1 mètre (100 cm) nous avons :
100 / (256/243) = 94,921875 cm la 1ere frette est positionnée à 94,921875 cm du chevalet
100 / (9/8) = 88,888... cm la 2de frette est positionnée à 88,888... cm du chevalet
etc.
Voilà !Gui Bryennes FraCasparis - Avec mes questionnements sur votre interprétation du monocorde et des intervalles qui en résultent ce qui vient c'est : quelle musique peut-il y avoir derrière ?
mathius shadow-sky - le monocorde ne servait pas à jouer de la musique, mais à accorder les voix (sur la gamme). Et l'apport essentiel de l'Ars Nova ne concerne pas la gamme, mais le rythme ; ajoutant la division binaire (imparfaite) à la seule division ternaire (parfaite) alors existante, de manière à créer des polyphonies rythmiques indépendantes pour chaque voix (voies) du choeur. L'Ars Nova marque le sens de la musique savante occidentale écrite qui évoluera jusqu'à l'écriture symphonique du XIXe siècle et jusqu'à l'indépendance de tous les pupitres dans l'orchestre au XXe siècle (Xenakis, Ligeti). Mais depuis la fin du XXe siècle, les moyens de son évolution ont été retirés par les politiques (de mise en esclavage intensif des populations = à ne pouvoir se figurer que vivre tributaire de l'argent et) à interdire l'accès des salles de concert aux compositeurs désobéissants à la norme classique du XIXe siècle. L'Ars Nova marque le passage entre l'homophonie (toutes les voix obéissant au même rythme harmonisé en accord « parfait » note contre notre = le contre-point) favorisée par l'Ecole de Notre Dame au XIIe et XIIIe siècle et la polyphonie par l'écriture indépendante des voix du choeur : la superposition du rythme binaire au rythme ternaire d'alors qui aujourd'hui se comprend en : 3 pour 2 (triolet sur duolet). Cette révolution obligea le choeur exclusivement masculin à devenir vocalement mixte (la mixité sexuelle du choeur ne date que du XIXe siècle - celle à l'école publique ? Après 1970 ! -) dont les voix hautes étaient confiées aux garçons prépubères « enfants » (= ceux qui ne parlent pas) de choeur (soprano, alto, jusqu'à la culture des castrats au XVIe et XVIIe siècle pour l'opéra) qui avec les voix masculines formaient le choeur à 3 ou 4 voies/registres : (sopranos +) altos + ténors + basses s'autorisant le décalage, des points à ne plus être les uns contre les autres. Plus tard au XVIe siècle le choeur se verra divisé jusqu'à 8 voix, voire des tentatives exceptionnelles de l'indépendance de tous les pupitres devenue courante pour la musique contemporaine au XXe siècle. L'arrestation de l'évolution de la musique savante (free jazz y compris) se réalisa par l'action de « la politique culturelle » à partir de la fin des années 70 du XXe siècle.
contact mathius shadow-sky pour commentaires et remarques
Théorie Harmonique des Champs Scalaires Nonoctaviants
les Eléments Harmoniques d'Aristoxène de Tarente datant de -330 avant Jesus-Christ publiés
re tour DANS LE CIEL, DU BRUIT DE L'OMBRE