Pour que les Champs Scalaires (Scalar Fields) soient opéra-tionnels, il faut un nombre suffisant d'opérations moteurs en matrices imbriquées qui génèrent ses propres métamorphoses. Les échelles (de hauteurs, de durées, d'espaces, de sonorités, etc.) sont les coordonnées quantifiées de nos évaluations sensibles (accrochées à des chiffres). Les échelles nous permettent de comprendre les différentes sonorités intentionnelles de la musique dans la constitution d'accords. Les échelles se calculent et se localisent grâce à notre capacité d'évaluation scalaire, grâce à la subtilité de notre écoute qui localise soit par la « couleur » (l'impression) soit par une approche quantitative (de différence analytique) ou les deux à la fois. La systémique en usage des hauteurs, dans une certaine allure, se distingue par ses « modes » qui servent (et renforcent) l'humeur (l'association d'un mode à un sentiment dans la tradition indo-européenne dont les Tziganes sont les transmetteurs) et, la systémique en usage des rythmes se distingue par ses « mesures » qui servent (et sollicitent) la danse : exemple les 3 temps de la valse, les 2 ou 4 temps du tango, les 4 temps du rock, les 5 temps des danses slaves, les 6 temps des danses arabes, etc. Nous pouvons aller beaucoup plus loin (découvrir de l'inconnu) en élargissant les champs de la musique. La systémique de la musique peut être subtilisée par l'élargissement et la multiplication des goûts « d'identifications d'échelles soniques dans un métasystème coordonné d'opérations d'autotransformations permanentes de ces échelles ». Le système devient métasystème (sans systématisme ni mécanisme automatiquement prévisibles) quand ses opérations fonctionnent quelque soit les variables opérées des données scalaires. C'est exprimé de façon un peu pompeuse, car la « vastitude des possibles » n'est pas encore cernée : le champ ouvert n'a pas encore de limite compréhensible.
La limitation d'un système : est sa systématique. La « carte » des Champs de Systèmes Scalaires topophoniques permet de s'en échapper. Systématiser une musique, c'est programmer sa mort prochaine. La « carte » (map) n'impose rien, elle propose un inventaire connecté des possibles musicaux disposés dans leurs mobilités; et dans laquelle chacun voyage en prenant sa propre direction (ses propres décisions ?). Aucun automate prévisible ne prend la place de l'humain imprévisible (pas de robotisme, nécessaire qui se prétend être des dieux). La musique n'est pas contre le prévisible (nécessaire à l'imprévisible), elle est contre l'ennui (de l'ordre et de la routine) du bruit de fond et du divertissement (la diversion familière). Le bruit de fond est une musique qui disparaît de l'écoute par sa présence reconnue puis oubliée. C'est en cela que la surprise reste le fondement même du sens de l'existence de la musique.
La limitation de la musique algorithmique (initiée par Pierre Barbaud dans les années 50) ou systémique est qu'elle ne peut accepter de situations imprévisibles. Une situation imprévue bloque irrémédiablement le système (« système d'exploitation planté ! »). La limitation de la musique algorithmique et systémique (calculée) est sa prévisibilité. Même complexifiée au maximum en y « injectant » de l'aléatoire, elle reste toujours prévisible grâce à la subtilité de notre écoute musicale. Mais l'intérêt du calcul pour la musique (comme le disait Michel Philippot) est de faire l'inventaire de tous les possibles qu'offrent les variables de la musique qui sont en invention permanente : ce qui fait que l'une des qualités essentielles de la musique est : d'être surpris/e, même à chaque écoute de la même musique. La surprise touche et provoque l'émotion et la jouissance émotive. Iannis Xenakis ne s'est pas trompé : il re-touchait toujours « à la main » (sans machines) ses partitions stochastiques calculées. La musique comporte la surprise prévue et la surprise imprévisible : l'imprévu prévu, la surprise qui s'attend pleine de désir : la jouissance et le prévu imprévu, la surprise qui ne s'attend pas : l'étonnement, l'abasourdissement, l'ahurissement, le bouleversement, l'ébahissement, l'éblouissement, l'effarement, l'émerveillement, l'étonnement, le saisissement, la stupéfaction, remplis d'émotion (: le contraire d'un cadeau est une punition qui pour le masochiste est un cadeau). Notre corps (de l'esprit, esprit du corps) synthétise un nombre invraisemblable d'opérations que le calcul peut difficilement dénombrer (inenglobable par sa raison) et que l'on nomme intuition, et cette intuition a une forme : celle de sa personnalité de celui ou celle qui fait ses choix. Nous considérons le calcul comme une carte nécessaire pour nous localiser dans les possibles. Cette carte, la plus exhaustive possible en fonction de nos désirs d'explorations, s'alimente constamment de nos découvertes. Dans ce sens, elle évite son obsolescence. Une telle carte n'existe pas (à sa conscience) ou pas encore ou de façon informelle (non identifiée) avec des tentatives éparses qui tiennent le temps du compositeur (théories et systèmes musicaux propres à chacun). L'écoute permet de distinguer des subtilités que le raisonnement permet de découvrir. C'est en ce sens que l'écoute est l'organe essentiel de la localisation musicale. Une audition qui n'entend pas est sourde, mais une audition qui ne peut écouter est un mort ou un esclave (du conditionnement de ses sens automutilés).
Les Champs Scalaires forment la carte des possibles de la musique,
du point d'écoute entendue d'ici et de là.
De la cartophonie....
1er accès au « réseau scalaire mouvant » (sans répétition comme le flux et le reflux [1])
Musique multiscalaire polyscalaire
Comme la polytonalité ou la polymodalité, l'idée d'une musique multiscalaire développe le concept du mélange à priori immélangeable de différences. La polytonalité reste « un mélange de différences ambigües » puisque les modes majeur et mineur transposés sont issus de la même échelle : celle des 12 1/2 tons divisant l'octave [2]. Dans le multiscalaire, l'idée est de superposer plusieurs échelles différentes (avec leurs modes inclus) pour obtenir une artmonie ou artpoly [3] (sonorités d'accords) jusque-là inouïe dans une écriture polyphonique (plusieurs musiciens). Le nombre d'échelles possible étant très élevé avec leur modalisation (les modes internes possibles), que le « tissage » de l'espace du temps des hauteurs en espace de connexion multidimensionnelle où une échelle correspond à une dimension, deux à deux, trois à trois, etc., jusqu'au nombre de musiciens (réels ou virtuels) de l'orchestre possible, est encore difficilement audible actuellement ou confondre cette audition à de la confusion. Un orchestre de 61 musiciens peut jouer au moins 61 échelles différentes en même temps qui se modifient dans le temps. Sans considérer la « perception conditionnée de fausseté » des agrégats ou accords perçus de l'orchestre qui est pour le compositeur : du perçu obsolète.
La notion de dissonance est malheureusement toujours d'actualité au XXIe siècle dans l'auditoire. La dissonance est encore confondue avec ce qui est désagréable à l'écoute, contre ce qui est agréable. C'est un conditionnement culturel (spatial) et historique (temporel) d'à peu près 300 années qui oblige le jugement à croire à la décision de ce qui est juste et de ce qui est faux (injuste pour justifier la correction punitive ?). La fausse justesse, d'une échelle tempérée de hauteurs approximatives, jugée juste. La notion de dissonance est le résultat d'un état d'esprit qui est gêné. Un état d'esprit qui se pose en victime de souffrances non désirées. Un état d'esprit qui se déconsidère pour se poser en victime. La douleur de l'imaginaire collectif. Mais ses souffrances sont cultivées par son intolérance cultivée dans le bain permanent d'une morale en opposition : soit du bon sentiment (la morale du bien) soit du mauvais sentiment (la morale du mal). Morale exclusive qui gouverne nos choix intolérants où aucune nuance n'a de place pour vivre un temps (de plus) de subtilités : de raffinements. C'est un esprit torturé qui ne peut se résoudre que dans le duel (la mise à mort) et dont la musique n'a cure. Il est clair que, pour que puissent se développer des musiques multiscalaires (dans la tolérance), la notion de dissonance/consonance [4] ne peut qu'évoluer vers plus de tolérance et d'ouverture d'esprit : pour donner à la musique plus de possibilités et de subtilités à goûter la musique. Nous pouvons grâce à cela, évaluer aujourd'hui le niveau primaire dans lequel nous nous situons.
...
1er mélange proposé
Superposition des 53 échelles nonoctaviantes découvertes à partir de la division de l'octave en : 96 (1/16e de ton), 90 (1/15e de ton), 84 (1/14e de ton), 78 (1/13e de ton), 72 (1/12e de ton), 66 (1/11e de ton), 60 (1/10e de ton), et 54 (1/9e de ton). Nous avons déjà vu ici les connexions possibles entre les échelles dans ces 8 familles assimilées à des aéroports constituant pour chacune un mode de correspondances : un par famille. L'étape suivante est de connecter les 8 familles de 53 échelles nonoctaviantes.
...
Comprendre le sens des Champs Scalaires (Scalar Fields)
L'esprit rationaliste déterministe veut prévoir, savoir à l'avance et précisément. En musique ça donne : des partitions à exécuter sans surprise : des musiques sans surprises. La musique, encore au XXIe siècle, utilise la théorie de la tonalité avec son échelle unique qui divise l'intervalle d'octave (de rapport 2) en 12 intervalles égaux (nommé mathématiquement par Pierre Barbaud : Z12) avec 2 modes : 1 majeur et 1 mineur qui se positionnent (se transposent) sur les 12 différents degrés de l'échelle (de 12 intervalles égaux divisant l'octave) pour devenir les 12 gammes du mode.
Pour mieux comprendre le sens de l'échelle dominante unique Z12 du monde occidental musical, on peut la comparer à l'horloge qui divise la durée du jour et de la nuit (d'une révolution terrestre) en 2 fois 12 parties de durées égales où les 12 heures correspondent aux 12 notes de l'échelle Z12. Comme une horloge, Z12 recommence le cycle atteignant 12 = 0 (modulo 12). Le « mode majeur » correspond à la suite des 7 horaires suivant : midi/minuit = 0h, 2h, 4h, 5h, 7h, 9h, 11h qui tourne sur lui-même dans sa transposition (une transposition à la tierce majeure +4 correspond à la suite (la gamme) 4h, 6h, 8h, 9h, 11h, 1h, 3h). Le champ scalaire propose un champ de différentes échelles cycliques qui ignorent l'octave. Elles sont au nombre de 53, issues de la division tempérée de l'octave jusqu'au 1/16e de ton (il sera intéressant d'augmenter leur nombre en calculant au-delà d'1/16e de ton).
Cette théorie musicale tonale est âgée de 300 ans (qui s'impose avec J.-S. Bach jusqu'aujourd'hui - top des ventes : classique -, bien que ça soit J.-P. Rameau qui ait conçu et fixé la théorie), et pratiquement tous les compositeurs occidentaux ont tenté de sortir de : l'enfermement cyclique de cette perpétuelle « réincarnation » posée sur le principe de l'attraction fusionnelle (un réducteur drastique aux raffinements sonores, à la subtilité d'écoute) [5]. Les programmes informatiques de musique sont en majorité assujettie à la théorie totalitaire de Z12. La raison est : il n'y a aucune autre théorie musicale, hors de la théorie tonale construite sur Z12, universellement reconnue en Occident. Ou, il n'y a pas la volonté (par incompétence et bêtise) de faire évoluer cette théorie : beaucoup de compositeurs de la seconde moitié du XXe siècle ont proposé des théories de sorties (notamment à travers les micro-intervalles, la musique stochastique initiée par Iannis Xenakis et les propositions hétérophoniques de l'école roumaine, etc. qui ont donné une forte tentative de sortie de la linéarité contrapuntique simpliste du Z12 octaviant). D'où la nécessité des Champs Scalaires qui développent la partie de ce que Iannis Xenakis a intitulé les « structures hors-temps » de la musique.
C'est la tâche que nous nous sommes imposée avec nos recherches qui proposent : les (la théorie des) Champs Scalaires (Scalar Fields Theory). Nous proposons une autre théorie qui épanouit les précédentes, qui ne détruit pas celles existantes, mais qui peut les rendre obsolètes, puisque la théorie des champs scalaires inclut la théorie de la tonalité. La Scalar Fields Theory élargit l'espace vibratoire mesuré de 1 (avec une seule échelle) à l'infini (avec un nombre infini d'échelles qui ne sont pas soumises à l'attraction, de l'octave).
L'absence de théorie reconnue ne signifie pas l'inexistence de théorie. Au début du XXe siècle, la recherche dans le monde des micro-intervalles était une voie possible pour sortir de la « fatalité » de la théorie tonale de passer entre les barreaux de la justesse tempérée). Des noms comme Ivan Wyschnegradsky en Europe et Harry Partch en Amérique ont tenté et utilisé 2 théories différentes tout en manquant du systématisme tonal pour que leurs théories se valident d'elles-mêmes indépendamment du compositeur ou qu'elles imposent une pratique fixant les opérations donnant le sens de sa nécessité pour les autres tout en donnant la possibilité de sa transformation (du système : du déroulement des opérations et de la modification de ses opérations). Les expériences de Wyschnegradsky et Partch sont parlantes, car elles proposent 2 idées différentes de division de l'octave : Wyschnegradsky divise l'octave dans le tempérament de la racine, jusqu'à la racine 72eme de 2 pour le 1/12e de ton et Partch divise l'octave dans l'addition de divisions jusqu'à 43 divisions inégales de l'octave (autour de 28 cent au-dessus du 1/8e de ton) à partir des calculs de Helmhost. Wyschnegradsky disposait des 10 échelles tempérées (intervalle unique) : 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10, 1/11 et 1/12e de ton. Partch disposait des 13 modes (intervalles multiples) : [6]. Wyschnegradsky fait construire avec Alois Haba un piano en quart de ton et Partch construit son propre instrumentarium. Wyschnegradsky compose à partir du système polyphoniste et Partch revendique la monodie comme mode compositionnel. Cette opposition qui n'en est pas une, opposait l'Amérique à l'Europe : « l'intonation juste » contre le « tempérament » injuste (seulement par une différence d'opération). Le tempérament tonal est injuste pour « l'intonation juste », car pour la transposition cyclique du mode, le 7eme harmonique naturel (si) doit être « ajusté » (baissé). Pour une oreille occidentale, le 7eme harmonique sonne faux. Conditionnement, conditionnement...
Toutes les gammes, autres que Z12, pour une oreille occidentale, sonnent faux.
C'est à ce point que l'on se rend compte de la puissance du conditionnement. Ce qui paraît « naturel » est en fait « cultivé » et « éduqué » [7].
L'esprit rationaliste déterministe siège dans l'assurance de quantités précises chiffrées. L'esprit empiriste improviste navigue dans le vague de sensations surprenantes. Avec une gamme de gris entre ces 2 extrêmes.
A quoi sert la théorie des champs du réseau scalaires ? A entendre ce qu'on n’entend pas. Et + à se déconditionner. Elle possède d'abord la fonction d'une table d'orientation pour voyager dans l'infinité des gammes possibles à former, une boussole multidimensionnelle. Pour l'instant notre écoute ne peut distinguer qu'en juste ou faux : où une seule échelle est juste (Z12) et toutes les autres sont fausses : ce qui est limité pour un esprit explorateur. La théorie des champs du réseau scalaires peut se représenter comme un ensemble de règles qui mesurent la distance (intervalle) avec des étalons différents (mètres, pieds, etc., et pour l'instant avec 53 échelles). Les champs scalaires en réseau (scalar system fields network) proposent un champ de différentes échelles reliées entre elles à différents degrés (horaires) dont l'attraction de l'octave (l'intervalle de rapport 2) est inexistante et formant différents champs par dimension d'échelle. 53 échelles nonoctaviantes liées entre elles forment un espace à 53 dimensions. Comme repère à tous les modes probables et possibles. Sachant qu'ils peuvent se construire sur plusieurs échelles (dimensions) à la fois. Le mode n'a pas l'imposition de se former sur une seule échelle comme de coutume avec Z12. L'exploration des modes dans le champ scalaire des 53 échelles nonoctaviantes n'a pas été encore systématisée (2013).
Je vois les champs scalaires en réseau comme un ensemble d'échelles (sur lesquelles on monte) flottant dans l'espace sans pesanteur (de l'octave), dont chacune, à au moins un degré commun avec une autre et permet des passages qui échappent à l'attention de l'une à l'autre en même temps. Les échelles du champ ne sont pas des gammes : les échelles ont la fonction de repères, les gammes se jouent, bien que les repères des échelles soient jouables (la gamme par ton de Debussy est une échelle). Le Scalar Fields est un système de localisation fréquentiel qui donne la possibilité de déconditionner son écoute et ouvrir son esprit vers un champ plus large sans attraction (bien que la réjouissance reste présente). La théorie des champs scalaire permet de mettre en fonctionnement le processus de déconditionnement de l'écoute, pour accepter les autres, entendre les possibles inaudibles et incalculés, autrement dit se conditionner à l'ouverture d'esprit de l'exploration. Pouvoir entendre ce que l'on n’entend pas.
L'horloge Z12 se cantonne au champ terrestre, l'horloge des champs scalaires se cantonne aux différents horaires des planètes découvertes, les horaires multiples des champs scalaires sans attraction ouvrent à une vie extraterrestre. La connaissance de ces différents horaires planétaires (attraction non attractée) permet le voyage dans l'espace extraterrestre. Cette ouverture à la connaissance facilitera le voyage spatial et l'acceptation des autres : dans les champs scalaires, il n'y a pas de fausses notes, il y a seulement des hauteurs perçues isolées qui n'ont pas été reliées à leurs échelles. La théorie des champs scalaires ouvre la capacité de vivre plusieurs horaires en même temps formant une carte spatio-temporelle interplanétaire.
OBSTACLES
Le premier obstacle à l'audition du champ scalaire autre que le conditionnement, est la lutherie. Tous les instruments de musique occidentaux manufacturés sont fixés à l'échelle unique Z12. Dont le piano, instrument majeur et couteux reste la référence de l'apprentissage de la musique en Occident. Ecoles (conservatoires) + éditeurs + luthiers + salles de concert forment un réseau fermé (comme la théorie tonale) qui n'accepte personne d'autre, autrement dit un régime de privilèges (voire raciste). La destruction de cette tradition n'est pas nécessaire pour que naisse la pratique de la théorie des champs scalaires. Il ne sert à rien d'obliger (ou d'interdire) celles et ceux qui ne souhaitent pas vivre l'expérience du voyage (spatial extraterrestre). Cette hégémonie traditionaliste nous oblige à aller voir ailleurs, hors du réseau : conservatoires + éditeurs + luthiers + salles de concert dédié à la musique "classique". Une organisation humaine non encore existante ayant la volonté d'élaborer des musiques inconnues à partir d'un système d'échange basé sur le même état d'esprit ouvert à l'expérience.
Mais il existe certains instruments de musique qui peuvent sortir de la théorie tonale de Z12 : certains instruments de musique extraoccidentaux (je pense au dan tranh, cithare vietnamienne avec ses chevalets mobiles). Les cordes (violon, alto, violoncelle et contrebasse) grâce à leur touches sans frettes, abusivement utilisées dans la musique classique (et de film) ont la possibilité de s'installer dans les champs scalaires, comme les trombones. L'autre possible, est de construire soi-même ses instruments de musique et/ou convaincre quelques luthiers à faire partie de l'aventure. La tendance du DIY (do it yourself) a élargi la pratique de l'instrument de musique objet par des musiciens concertants, développé après la musique concrète. Mais le jeu des instruments-objets souvent échappe à l'accord qui n'est pas leur première raison de sonner (du moins pas encore). Les synthétiseurs au protocole MIDI ont pratiquement tous la possibilité de se réaccorder (c'est à partir du DX7 que beaucoup de programmes de réaccordage ont vu le jour). Certains instruments virtuels informatiques acceptent le protocole Scala. Le sampler (échantillonneur) reste l'instrument le + capable pour élaborer des orchestres virtuels de sons-instruments accordés sur les champs scalaires.
Mais tous ces instruments de musique pouvant exploiter les champs scalaires sont encore aujourd'hui difficiles à assembler en orchestre (acoustique autonome). En attendant, je me rabats sur l'orchestre virtuel (ovo) produit avec un ou plusieurs samplers. La diffusion de la musique des champs scalaires avec des samplers demande obligatoirement l'énergie électrique, et un système de diffusion par haut-parleurs, ce qui pour une musique de trajectoires multiples dans l'espace tridimensionnel permet d'entendre des sont d'instruments (ou isolés) qui viennent de partout en se déplaçant partout. Mais quand même, jouer avec des musiciens a plus de chance d'atteindre le sublime qu'avec des machines.
...
En quoi les échelles nonoctaviantes sont-elles une (r)évolution majeure ?
elles ne tournent pas autour du pot, elles l'emmènent.
Bien qu'elles en soient issues du tempérament égal (divisions égales d'un cycle) puis d'un noncycle (voir Ourdission 41), les échelles nonoctaviantes n'ont pas d'équivalent historique. L'idée forte est de comprendre que n'importe quel intervalle autre que l'octave peut être cyclique ou noncyclique et être divisé en un nombre quelconque de degrés en évitant les intervalles « habituels » (les intervalles trous noirs épuisés, retenus jalousement aux dépens des autres parce qu'on les croit « naturels » ou « consonnants » qui relève d'un conditionnement et d'une fermeture d'esprit). L'organisation des degrés (notes, hauteurs, pitch) d'un grand nombre d'échelles (localisatrices de modes) en harmonie (accords) ou artmonie (ensemble en même temps) crée le réseau des liaisons multiscalaires qui forment le Champ Scalaire (ensemble de toutes les échelles en réseau en mouvement artmonique qui localisent tous les modes et ses positions, les gammes. Le Champ Scalaire est l'espace de transformations de toutes les échelles, modes et gammes. Des mutations de tous, et toutes autres opérations possibles de transformations. Exemples : échelle à intervalle mobile qui se fixe sur un mode multiscalaire, un mode multiscalaire qui se transpose sur une échelle étrangère, une échelle nonoctaviante et noncyclique qui se transforme par réduction de son intervalle pour devenir cyclique puis un mode, etc.).
La nécessité de changer et d'utiliser d'autres échelles que celle de Z12 c'est affirmé au début du XXe siècle (si Z12 persiste, c'est grâce à l'esprit conservatoire).
La nécessité d'utiliser des échelles nonoctaviantes s'impose au début des années 80 du XXe siècle avec entre autres la possibilité d'utiliser et le fréquence-mètre (d'où le calcul en fréquences des échelles) et les synthétiseurs numérique (DX7) pour chiffrer le phénomène (l'échelle convexe nonoctaviante de ma guitare électrique est conçue à l'oreille). La notion de nonoctaviation a été introduite et affirmée par Ivan Wyschnegradsky en 1953 (avec la 3eme version de sa « Loi de la pansonorité »). Il se rend compte que l'octaviation peut être évité avec l'utilisation des échelles microintervallaires : elle va même de soi (l'octave disparait dans l'abondance de notes). Il introduit 9 échelles à l'usage divisant l'octave par : 24 <=> 1/4 de ton ; 30 <=> 1/5e de ton ; 36 <=> 1/6e de ton ; 42 <=> 1/7e de ton ; 48 <=> 1/8e de ton ; 54 <=> 1/9e de ton ; 60 <=> 1/10e de ton ; 66 <=> 1/11e de ton ; et 72 <=> 1/12e de ton. Bien qu'il n'est jamais expérimenté à l'oreille que le 1/4 de ton avec son piano en quart de ton, Wyschnegradsky a pris conscience de la nécessité de la nonoctaviation pour sortir du système Z12 avec les micro-intervalles tempérés. La réalisation audible d'échelles autres que Z12 a pu vraiment se réaliser avec l'apparition des synthétiseurs analogiques et Wendy Carlos (« Switched-On Bach ») en 1985 propose 3 échelles nonoctaviantes : Alpha (α) qui divise une quinte harmonique (3/2) en 9 degrés, Beta (β) qui divise une quinte harmonique (3/2) en 11 degrés, Gamma (γ) qui divise une quinte harmonique (3/2) en 20 degrés. L'ambitus de 5te pour Wendy Carlos est le moyen le + simple pour éviter l'octaviation [8] et un retour à « la suite des 5tes » de la Grèce antique ? Un peu avant en 1982, je propose Oudission 41 et ses dérivés d'échelles nonoctaviantes noncycliques et premières (où la division de l'ambitus s'opère avec un nombre premier) puis les 53 échelles nonoctaviantes issues des divisions octaviantes (de 1/16e de ton à 1/9e de ton) destinées entre autres à l'écriture Ondale (forme d'écriture de la musique qui privilégie la polyphonie d'arpèges qui sied aux métamorphoses multiscalaires). L'idée du Champ Scalaire émerge avec l'utilisation intensive de plusieurs échelles nonoctaviantes en même temps par différents instruments (on imagine le laborieux de l'interprétation à l'orchestre, même avec un fréquence-mètre : XØ pour orchestre [1983] reste inachevé pour cette raison). La multiscalarité numérique me fut rendue possible avec l'apparition du sampler (échantillonneur numérique) [9] en plus des synthétiseurs analogiques [10] et numériques. Notons que le groupe de musiciens The Residents utilise systématiquement sans le théoriser depuis les années 70 du XXe siècle des échelles et modes qui évitent l'octave (avec humour).
Nous avons constaté que l'octaviation est une exception pour un cycle scalaire. A part pour l'intervalle d'octave lui-même de rapport 2, l'octaviation est une exception ; car n'importe quelle division de n'importe quel autre intervalle devrait se retrouver majoritairement dans l'octaviation, mais ce n'est pas le cas.
Exemple
En considérant la division de 3 à 56 degrés du second intervalle de la série harmonique : la quinte [11] harmonique 3/2 = 1,5 et tempérée (12√2)7 = (1,0594630943592952645618252949463)7 = 1,4983070768766814987992807320298... [12] Ces 54 premières divisions scalaires de la quinte (sachant que 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53 sont des nombres premiers) sont majoritairement nonoctaviantes.Voir les 56 divisions (-2) de la quinte, dont 46 échelles sont nonoctaviantes (sur 8 octaviantes)
&
Téléchargez les 46 premières échelles nonoctaviantes divisant la 5te (46 Scala files zip 20Ko)Sur 54 échelles divisant la quinte, 8 sont octaviantes et 46 ne le sont pas.
La nonoctaviation permet de se rendre compte que le rapport 2 n'est pas dominant dans le nombre d'échelles possibles. La fusion octaviante qui permet d'unir des instruments différents en une seule sonorité indissociable est une exception. La pensée nonoctaviante permet de distinguer les différences dans les alliages sans que les particularités disparaissent pour ne former qu'un seul objet. L'idéologie de la « fusion » dans l'un, nous vient tout droit des croyances déïques monothéistes qui est à ne pas à confondre avec le mysticisme s'entendant (s'artmonisant par nos sens sacrés - non profanes - dans notre contexte vital nonartificiel). La pensée nonoctaviante offre un autre aspect idéologique, celle de montrer que toutes les différences peuvent ensemble s'entendre.
Le champ scalaire nonoctaviant permet aussi l'affinement de l'écoute : accepter que d'autres échelles que Z12 ne soient pas « fausses », mais différentes. Aujourd'hui, très très peu d'auditeurs peuvent distinguer la différence d'une échelle nonoctaviante à l'autre. Cette éducation de l'écoute (ouverture d'esprit à la différence, sans se terroriser ni se braquer) justifie de mieux s'entendre pour s’accorder sur tous les tempéraments possibles.
Dimensions supplémentaires
A nos 53 échelles nonoctaviantes découvertes à travers les multiples des divisions du ton :
1/16e, 1/15e, 1/14e, 1/13e, 1/12e, 1/11e, 1/10en et 1/9e de ton ; nous avons :
29 - 3 = 26 échelles nonoctaviantes supplémentaires issues de la division de la quarte
46 - 3 = 43 échelles nonoctaviantes supplémentaires issues de la division de la quinte
31 - 6 = 25 échelles nonoctaviantes supplémentaires issues de la division de la sixte mineure
en attendant les autres ...53 + 26 + 43 +25 = 147 échelles nonoctaviantes disponibles dans le champ scalaire (en attendant +) formant un espace à 147 dimensions (pour l'instant)
...
Théorie des champs scalaires (le jeu des connexions polyscalaires)
Un champ scalaire se définit (comme un espace qui se localise) par ses coordonnées. Les coordonnées sont représentées par les échelles qui constituent le champ. Une échelle est une référence mobile qui ne se localise que pour elle-même où sa position importe moins que son rapport quantitatif - l'intervalle - qui l'identifie. Tout intervalle possède une sonorité identifiable (ou du moins nous le projetons comme tel). La sonorité de l'intervalle définit la sonorité de l'échelle et la localise. Un champ se construit avec plusieurs échelles. Leurs degrés communs communiquent avec les autres échelles par des passerelles. Ces passerelles que nous avons nommées « modes de correspondances » forment l'intersection (opération de la théorie des ensembles) qui permet les liaisons entre les échelles. Le champ s'anime avec l'usage de ces liaisons de correspondances qui donnent la possibilité de former des accords interscalaires (accords dont les degrés proviennent de différentes échelles) qui opèrent diverses relations (toujours identifiées par les différentes sonorités).
Etablissement du champ scalaire nonoctavian [phase 1]
Nos premières découvertes nonoctaviantes à partir des divisions du ton (200 cents) nous ont amené à 53 échelles dans 8 groupes (de 1/16e de ton à 1/9e de ton)
1. connexion des 8 modes de correspondances résultants des 53 échelles nonoctaviantes issues de la division du ton (premier acte d'éloignement de Z12)
pour la suite, nous allons établir la
2. connexion des 53 échelles nonoctaviantes
et montrer les
3. projections modales des connexions possibles
pour obtenir des
a. modes monoscalaires (modes formés d'une seule échelle)
b. modes polyscalaires (modes formés de plusieurs échelles, au moins 2 pour duoscalaires, 3 pour triscalaires, 4 pour quadriscalaires, etc.)
Un champ scalaire donne la possibilité de connecter toutes les échelles, formées (reconnues) par la sonorité propre de leur intervalle. Les 3000 échelles recueillies par Manuel Op de Coul, audibles avec son programme Scala peuvent former un champ à partir du moment où elles se connectent ensemble pour former des accords « collatéraux ». Comme pour une échelle, la constitution de l'identité d'un champ scalaire dépend de son usager : par le nombre d'échelles, par le nombre de connexions, par le nombre de modes en connexions, par le type de gammes qui se disposent et qui se transposent et d'accords connectés qui le constituent et le génèrent.
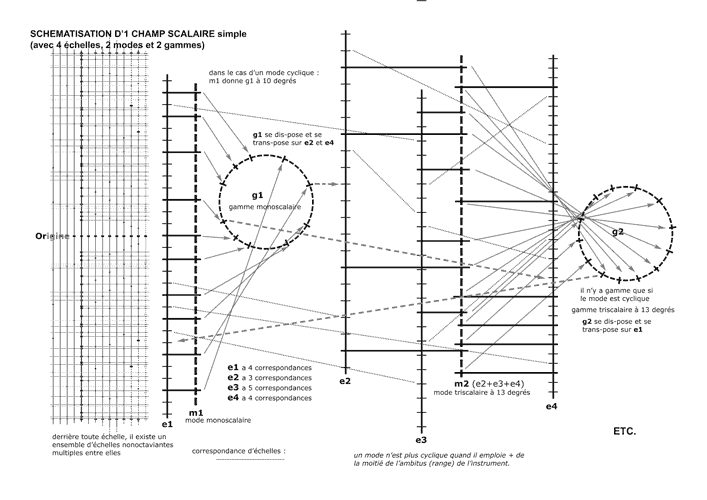
Je pense qu'un graphique permettra de mieux comprendre le propos du Champ Scalaire :
On imagine les connexions entre 53 échelles nonoctaviantes (+ les 22 supra apparentées à la quinte = 75 échelles) donnant différents échanges et métamorphoses avec des modes monoscalaires et polyscalaires et cycliques et noncycliques avec un ensemble de gammes qui se transposent sur des échelles autres de celles qui l'ont constitué, est un exemple d'un champ scalaire possible. La complexité d'un champ scalaire par l'abondance se simplifie par l'écoute. C'est l'écoute qui décide dans la sonorité de ce qui satisfait ou pas, de ce qui est retenu ou pas pour former un champ particulier.
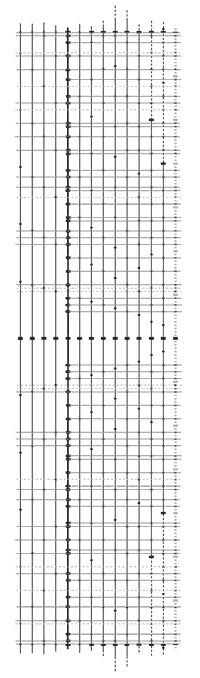
Rappelons qu'un groupe nonoctaviant (avec une même origine) ressemble à ça :
Une échelle nonoctaviante comme toutes les autres, n'est jamais vraiment isolée, elle est toujours apparentable (multiple) à un groupe qui lui ressemble. C'est cette apparenté (incluant la liaison des contraires) qui permet de créer des liens qui forment le champ scalaire (et l'anime).
...
Fonction des Champs Scalaires Nonoctaviants
Dans la constante et la variation
L'humain nécessite une constante pour percevoir la variation. La variation sans référant est inévaluable ou cette variation constante devient la constante elle-même : musicalement une monotonie bien qu'elle soit hétérogène ; où il faut reconstruire « par dessus » une autre variation à partir de l'hétérogénéité perçue constante (homogène). En musique, la « basse continue » ou la « fondamentale » harmonique détiennent le rôle de la constante sur laquelle le « chant » ou le « solo » se repose. À l'unisson de l'octave qui « enfle » l'amplitude, nommé « phénomène de résonance », sortir du retrait du repos de la résonnance du doublage confirme la variation qui est l'état primordial de la nonoctaviation.
Le champ (invention mathématique du XIXe siècle) est un concept de base pratique pour mettre en relation plusieurs constantes. La constante du champ scalaire est le groupe d'échelles nonoctaviantes choisies jouées ensemble dans l'interaction formant le champ. Une échelle est une suite de fréquences équidistantes du même intervalle puis une suite de sensations de hauteurs définies par une sonorité (celle de l'intervalle la constituant). Les hauteurs (pitch) sont les points-cibles fréquentiels connectés pour assemblage d'accords de la synthèse additionnée. Ces connexions forment les ponts des méta-morphoses à la fois d'échelles à échelles et de champs à champs (trans-formations) et les agglomérations des accords de l'harmonie contextuelle définis par ses trans-connexions. Un champ entier peut devenir une constante d'autres champs connectés.
C'est par le principe de différence et répétition pour le temps et de constante et variation pour l'espace que les champs ne peuvent qu'être pluriels. La limite de perception différentielle est étendue et dé-tendue à partir du moment où le champ variant devient constante pour révéler d'autres champs en interactions. Ça signifie que tirer une corde ou impulser une tension ne génère pas un son (l'objet de son écoute : son effet) mais un amas de conséquences dont certaines restent imprévisibles (non préaudibles et nonentendues) un amas de différences fréquentielles qui forme l'harmonie des champs scalaires et non plus des hauteurs d'un son.
Il ne s'agit plus d'homogénéiser (de « purifier » aïe) dans l'unité de l'ordre, du symétrique, reflet de son obéissance qui reproduit par la copie l'ensaignement qu'il a reçu pour n'exprimer que la constante pour réduire la diversité à quelques élus dominants, mais bien de surprendre par des surprises inattendues la diversité encore inconnue qui exerce l'audition à l'inentendu : son ouverture à l'inconnu, à l'étranger qui annihile tout racisme (toute réaction de terreur panique dans l'institution théorique pour la musique).