Exploration scalaire

d'autres sonores nécessaires à l'ouverture d'esprit

à la découverte d'échelles inouïes

 

C'est à l'écoute de la « gamme par ton » de Debussy (qui a coloré toute la musique impressionniste du XIXe siècle) que j'ai pris conscience de l'importance de la sonorité des échelles. Cette gamme est en fait une échelle de l'octave divisée en 6 intervalles similaires (nommée mathématiquement 200 cents et 2^1/6 ou ⁶√2 = 1,12246). Au conservatoire de Varsovie, je fus impressionné par l'extrême variété des modes de la musique des Tziganes de l'Est : où presque chaque état d'âme a son mode musical. Les modes de la musique indienne dont les modes tziganes sont dérivés sont élaborés dans le même sens. Bêla Bartók en a recueilli quelques-uns en Roumanie, Bulgarie et Hongrie. Je découvris ensuite les modes à transpositions limitées d'Olivier Messian et les manipulations scalaires de Iannis Xenakis et l'algorithmie de Pierre Barbaud, reprises et développées par André Riotte : tous ces arrangements de hauteurs, impriment impressionnent des sensations différentes, dans notre système de projections perceptives des sonorités. Une même musique avec une gamme différente, change (voir infra avec la valse de Chopin) : elle n'est pas perçue et reçue pareil : les proportions et ses attachements émotionnels sont perturbés [1].

Ce qui nous intéresse dans l'utilisation de la multitude d'échelles possible, ce sont les sonorités de chacune d'elle (contrairement à l'humeur qui identifie une émotion). Chaque intervalle possède sa propre sonorité (jusqu'à la limite du spectre imprévisible des 2 sons constituants l'intervalle) : une identification de sensations particulières propre à chacun. Aussi la possibilité mathématique de leurs mutations. La composition des intervalles constitua le premier pas vers une musique savante, celle d'élaborer un système abstrait d'échanges et de passages pour la composition de musiques très diverses au-delà du simple accompagnement « à la fondamentale » du chant. Le système tempéré de 12 tons a fait son temps depuis plus de trois siècles : c'est un système qui a permis ses passages et ses déplacements (transpositions, modulations, etc.), mais qui reste clos sur lui-même : il fut élaboré et construit sur deux modes : le majeur et le mineur. Depuis le début du XXe siècle, les compositeurs à partir des propositions de Schoenberg et Wyschnegradsky essayent de proposer autre chose. Où l'un proposa un nouveau système avec le dodécaphonisme et l'autre proposa « une multiplicité de milieux sonores tempérés ultrachromatiques à base de micro-intervalles » (J.E. Marie) [2]. C'est le début de la révolution musicale permanente que traversent un Stockhausen, un Cage et qui se confronte jusqu'à aujourd'hui à une résistance farouche de la « tradition tonale » qui garde malgré tout sa domination dans la création contemporaine. C'est le paradoxe contemporain de l'histoire occidentale de la musique, qui depuis son origine offre une succession de musiques qui se renouvellent par l'apport de sonorités et de savoir-faire compositionels différents parfois inattendus. Une tradition historique occidentale du renouvellement artistique brisé par l'exploitation de la rentabilité médiocratique d'aujourd'hui.

Diviser les cordes pour créer des échelles et des modes musicaux est une pratique de la Grèce antique (ton vient de tendre une corde musicale). Elle est toujours en pratique de nos jours plus de 2500 ans après. La culture en Chine est beaucoup plus ancienne, pour former des modes de hauteurs elle ajustait des bambous, les cordes aussi tout comme la culture de l'Inde sur des proportions. Les Tziganes ont modifié et transporté ces modes vers l'Europe. Pourquoi n'avons-nous retenu que deux modes (majeurs et mineur) des dizaines de modes amenés par les Tziganes de l'Inde ? Pourquoi durant toute l'histoire occidentale de la musique, tous ajustent des gammes de hauteurs (musiciens et non-musiciens) ? Pourquoi aussi Z12 (12 divisions équidistantes de l'octave = le demi-ton tempéré nommé ainsi par Pierre Barbaud) en 300 ans c'est imposé au détriment d'autres échelles ? Pourquoi est-il tant difficile de sortir de Z12 ? Pourquoi toutes les autres échelles autres que Z12 sonnent faux ? [3], etc.

Ce que nous proposons ici à la suite de ceux cités supra : à partir d'une exploration systématique des échelles et de leurs propriétés (puis de l'arrangement modal et de leur transposition en gammes, etc.), est d'extraire un système ouvert pluridimensionnel en fonction de nos découvertes. Nous sommes avides d'ajouter un nombre de sonorités nouvelles et d'y naviguer au prorata du nombre de combinaisons d'intervalles possibles, c'est-à-dire à l'infini : sans fermeture pour découvrir d'autres sensations d'accords vibratoires. Nous nous orienterons plus vers la prospection des échelles asymétriques inouïes avec et sans redondance (cycliques et non-cycliques) où les intervalles basiques de la série harmonique seront évités : leur forte prégnance fait masque aux autres encore inconnus. Nous essaierons de retirer le voile aux à priori simplistes de la perception de « hauteurs absolues » pour proposer une mobilité permanente dans les connexions systémiques des hauteurs qui ne le deviendront plus par leurs multidimensionnalités [4] [5].

A quoi sert cette architecture mouvante que nous nommons pompeusement Champs Scalaires (Scalar Fields) ?
A créer des tapis mouvants de jeux, pratiques pour la composition musicale immédiate asystémique afin d'entendre puis d'écouter d'autres choses, dans la délectation.

Pourquoi utiliser en musique d'autres échelles que les 12 degrés (tons) tempérés adoptés depuis le XVIIe siècle, nommés aussi « gamme chromatique » qui inclut le « mode majeur » pour lequel toute notre notation et attention musicale occidentale lui est consacrée ? Le « mode majeur » à 7 degrés comme son nom l'indique reste dominant : il inclut le mode « barbare » pentatonique à 5 degrés utilisé dans différents accords par différentes cultures de la planète. Les « modes mineurs » sont des « altérations » du mode majeur : des ersatz. Pourquoi lui adjoindre d'autres modes pour lui retirer sa domination ? Tout lui est destiné : le nom de ses notes (do ré mi fa sol la si do ou A B C D E F G), la notation sur la portée de 5 lignes avec ses clefs. Pourquoi évoluer ce système dominant qui est utilisé depuis plus de 300 ans ? Envoyez-moi vos réponses s.v.p.

Nos consciences évoluent (par la force de l'âtre) de l'uni au pluri, de l'universel au pluriversel : c'est une préparation à la future organisation de l'humanité qui passe par la musique, où « un seul ne gouvernera plus tous ». Causes et effets ne sont pas uniques, mais multiples (je poursuis ce que Gilles Deleuze posa comme jalon et d'autres avant comme Nietzsche ou Spinoza). L'évolution de notre système à domination vers un système qui permet le choix, qui permet à chacun de choisir. Ces choix possibles qui ouvrent nos esprits à la multiplicité pour cultiver notre intelligence et non à la bêtifier dans la domination par l'unicité. Nous savons maintenant que la domination est un frein à la culture de notre intelligence humaine et l'évolution de l'humanité ne peut pas être maintenue à l'arrêt.

Aujourd'hui, le piano n'est plus l'instrument de musique universel clamé au XIXe siècle. L'échantillonneur numérique l'a surpassé. Et, pour la première fois dans notre histoire humaine, les spéculations théoriques sur les gammes sont devenues accessibles à l'audition dans l'immédiat; sans être obligé de construire ni de calculer un instrument de musique approprié. Les instruments de musique numériques (pas tous malheureusement) invitent à d'autres tempéraments, d'autres modes avec l'aisance qui n'existait pas avant le DX7 II (synthétiseur de synthèse par modulation de fréquence développée par John Chowning et réalisé par la compagnie japonaise Yamaha en 1983). Dans ces pages nous vous donnons la possibilité de « goûter » aux échelles nonoctaviantes avec vos instruments de musique numériques qui le permettent.

Mais, l'utilisation de telle ou telle échelle (mode, gamme) dépend fortement du contexte musical et du rendu désiré et visé. C'est l'échelle qui s'adapte au contexte du possible de l'instrument de musique bien que le contraire doit être envisageable pour l'évolution de ces instruments. Aussi l'utilisation d'autres échelles (modes, gammes) demande un entrainement pour la mémorisation, la correspondance et l'émission musicale (je pense au champ de liberté de la voix). Une échelle (ou plusieurs ou son champ de systèmes scalaires) peut se trouver appropriée pour tel contexte instrumental et inapproprié pour un autre. Exemple. Je voulais me rendre compte si la limite de perception des différences évaluée par Carillo à 1/16e de ton et par Wyschnegradsky à 1/12e de ton pouvait se vérifier au-delà. J'expérimentais l'échelle de 1/17e de ton avec un sinus accordé à 440Hz. Le résultat qui m'interpella fut de me focaliser sur une variété de battements dans différents accords où les différences sont audibles. Et 1/17e de ton parait grossier dans ce contexte qu'il est possible d'affiner. Une échelle aux intervalles progressifs devient nécessaire afin d'accorder les vitesses de battements des fréquences basses (plus lentes) à celles aigües (plus rapides). Dans quel autre contexte peut cette échelle être adaptée ? Téléchagez ce prêt-à-musique pour le sampler Kontakt2 (multi 13Ko) : un prêt-à-musique libre de droit à ne pas utiliser tel quel mais à personnaliser, et envoyez-moi vos adaptations audibles.

 

 

Notes
[1] La représentation harmonique (puis spectrale) de la superposition des sons simples est la suite logique de la pensée d'Aristote puis des polyphonistes de la « renaissance » et de la pensée exacte de Jean-Philippe Rameau « des lumières », qu'il développe dans son traité : « Nouvelles réflexions sur le principe de l'harmonie » en 1752 ou 1722. La décomposition d'un son complexe en plusieurs sons simples de Fourier (des sinus pour la représentation FFT : Fast Fourier Transform) où chaque fréquence sonique coïncide à une ligne et la superposition de ces lignes forme un spectre de fréquences harmonique ou non (un ensemble de fréquences distinctes qui caractérisent en partie la reconnaissance possible de ce son : mais cette représentation sonique des fréquences vibratoires reste incomplète pour permettre une reconnaissance de ce son. Citons pour exemple les programmes ou synthétiseurs de resynthèse spectrale d'un échantillon sonique enregistré : le son resynthétisé ne ressemble pas au son enregistré, mais l'imite.). Ce type de conception à permis d'imaginer la synthèse additive dont le premier instrument résultant est l'orgue jusqu'aux différentes synthèses analogiques d'hier et numériques d'aujourd'hui. Dans notre idée des Champs des Systèmes Scalaires (Scalar System Fields), les synthèses se fondent dans leurs scalérisations multidimensionnelles et perpétuellement mobiles.
[2] La première incursion dans le micro-intervalle occidentale s’est produite dans la continuité de la division tempérée de l’octave (rappel : le tempérament permet la modulation dans différentes tonalités en altérant et ajustant les intervalles harmoniques afin qu’ils puissent se correspondre à différents registres cela par une division exacte de l’octave). Des précurseurs comme Haba, Carillo et Wyschnegradsky cités par Jean Etienne Marie ont continué la division du ton tempéré : du ton entier jusqu’au 1/16e de ton (considéré comme le plus petit intervalle de hauteur perceptible pour les oreilles fines et entraînées). [Nous savons que la distinction du plus petit intervalle dépend de la texture du son. Avec certains sons la perception d’un intervalle reste floue ou difficilement discernable alors qu'avec d’autres il se distingue très bien. C'est une proportion entre la densité sonique d'un son et le plus petit intervalle de hauteur détectable. Ces derniers sont retenus pour la distinction des intervalles de l’échelle et les autres pour former des amas ou agrégats de masses sonores pour un jeu toujours sur la sonorité.]
[3] nous pourrions déjà répondre à ces trois dernières questions : le système tonal est d'une grande souplesse et permet des modulations et des transpositions (des changements de sonorités dans le système d'une même et unique échelle : Z12) que le dodécaphonisme par exemple ne permet pas, malgré ses innombrables combinatoires il n'a qu'une sonorité. Le système tonal permet l'atonalité dont elle fait partie ainsi que le dodécaphonisme de Schoenberg et la gamme par ton de Debussy, même les modes à transpositions limitées de Messian sont inclus dans le système tonal et tous les essais d'accords de l'échelle Z12 de Pythagore, Zarlino, mesotonic, Werkmeister, Salinas, Kirnberger, Rameau, etc. dont aucun ne touche à la "stabilité" sonnante du mode majeur. Si Z12 règne toujours c'est que l'on a pas trouvé mieux à sa souplesse opérationnelle fermée : un système qui permet de moduler de transformer, de transposer, etc., d'échelles, de modes, de gammes pour développer un grand nombre de sonorités scalaires sur lui-même (qui compte 3301 modes de 5 à 12 tons) et dont chacun tourne autour sans s'en détacher. Nous nous efforçons de proposer ici avec nos Champs des Systèmes Scalaires (Scalar System Fields) une ouverture. Au-delà d'un système de « hauteurs » tonales fixes, nous désirons un métasystème mouvant de forces centripètes et centrifuges multiples. Si les autres échelles autres que Z12 nous « sonnent fausses » c'est bien à cause de 300 années de culture univoque dans un système devenu autoritaire par autocratie (qui se retrouve dans le système même, avec des mots comme « dominante », « sous-dominante », « sensible », etc.).
[4] nous avons plus d'une trentaine d'années d'exploitation exploratoire d'échelles inouïes désystématisées, mais tout comme nos prédécesseurs, nous n'avons pu insuffler un intérêt pour ces recherches à sonner autrement (la résistance des habitudes). Même avec l'apport de l'informatique, les possibles restent faibles et à l'état de bricolage et de bidouillage : en trente années il n'a existé aucun programme de construction de systèmes ouverts d'échelles en temps réel pour la composition musicale, malgré quelques essais inachevés. Ce type de programme permettrait un accès aisé et articulé à travers divers systèmes actifs au monde interactif des échelles, modes, gammes de hauteurs toujours en mouvement grâce à ses nouvelles opérations en interaction suivant les qualités sonores des sons mis en mouvement et que nous tentons de découvrir ici. Notons que Harry Partch (1901-1976) est le compositeur connu qui poussa le plus loin la réalisation d'un autre système de hauteurs avec son orchestre d'instruments dédiés.
[5] Nous ne ferons pas une incursion dans les mathématiques profondes pour devenir incompréhensibles au musicien. L'avantage de la musique est l'expérimentation immédiate sonore des calculs spéculatifs et exploratoires. Et nous tiendrons tout le long de nos explorations à rester un homme musical.

.

.

exploration de l'outil des briques d'Alger

LA FORME DIVISIONNAIRE DE L'OUTIL

 

Mettre en question le principe opératoire

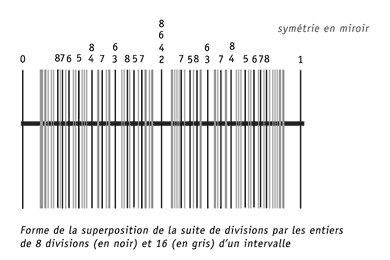
La forme opératoire est l'outil qui permet l'exploration et la représentation de la découverte. Mais la découverte est intimement liée à l'outil qui l'a découvre. Nous voulons dire que la forme de ce qui est découvert aura obligatoirement la forme de l'outil qui le découvre. C'est en ce sens qu'il est important de multiplier des outils différents pour une même tâche afin de se rendre compte des résultats différents de la même découverte. Exemple l'outil : division (qui est un opérateur). Nous constatons que la superposition de divisions par la suite des entiers { 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; 10 ; 11 ; 12 ; 13 ; 14 ; 15 ; 16} donne une forme identifiable, en miroir (symétrique) unique. Quel que soit le nombre de divisions, la forme reste identique. Cela confirme qu'une suite d'entiers divisant ne donne pas un résultat linéaire. Pourtant, cette forme opératoire est utilisée pour tous les éléments de la musique : la division des intervalles de « hauteurs », la détection les échelles tempérées, la formation des intervalles de durée : des valeurs rythmiques rationnelles (tels que : le duolet, triolet, quartolet, quintolet, sextolet, septolet, etc., ou la métrique avec ses mesures à 2, 3, 4, 5, 6, 7 temps, etc.). Ces divisions opératoires servent aussi à localiser les positions des harmoniques sur une corde ou un tube, etc. Elle fait tout, mais les divisions paires, impaires ou premières (par les nombres premiers) donnent des résultats différents dans sa même forme donnée [1] :

 

La représentation de la forme géométrique de la division n'est pas équidistante comme nous aurions tendance à le penser des expériences perceptives. Plus les divisions sont grandes plus elles sont resserrées entres elles. C'est une forme unique qui donne à percevoir dans le même sens. Notre question est : y a-t-il d'autres formes divisionnaires ? Et si oui comment sont-elles percevables dans un même contexte ? Comment peut-on les représenter ? Nos perceptions logarithmiques peuvent-elles avoir une différence (-) exponentielles, un inverse (1/x) et un inverse de la différence (-1/x) par exemple, pour rester dans le domaine des opérations simples ?

ou ?

A gauche, une progression logarithmique qui correspond entre autres à la série harmonique calculée à partir de la vibration perpendiculaire unique d'une corde tendue.
A droite, une progression exponentielle qui correspond entre autres à la série des durées à partir de la quadruple croche comme unité et à l'inverse négative de la série harmonique.
Dans l'esprit d'une échelle exponentielle opposée à la série harmonique, j'ai accordé ma guitare électrique dans ce sens : une échelle convexe où les intervalles s'élargissent plus ils montent dans l'aigu et à l'opposé, une échelle concave où les intervalles rétrécissent plus ils montent dans l'aigu. Grâce au chevalet sur rail : vers la page de l'accord de ma Météor

ou ?

les échelles élastiques progressives sans attraction sont l'une des finalités du projet

Il ne faut pas confondre :

la forme perceptive de l'équidistance,
la forme de la quantification,
la forme de ce que l'outil implique,
la forme du conditionnement,
la forme des suites d'intervalles.

Les nombres négatifs ont été difficile à admettre : leur admission n'a que 200 ans sur plus de 4000 ans de mathématiques. De là à admettre une harmonie négative possible dans un champ fréquenciel unidirectionnel (perçu du grave à l'aigu) semble jusqu'à ma mort improbable.

 

[

compétition artistique inutile Amérique versus Europe

Pendant une courte période du XXe siècle, l'outil division des intervalles de hauteurs, a formé deux tendances : l'une en Europe et l'autre aux Etats-unis. En Europe, la tendance était d'utiliser l'outil racine √ pour une division équidistante de l'octave. Aux Etats-unis, la tendance était d'utiliser l'outil fraction dans la continuité de la formation des intervalles de la série harmonique à partir des recherches du compositeur Harry Partch issues des travaux de Hermann Helmholtz (qui ignore l'opération racine). Ce mouvement se nommait « intonation juste » en réaction à « l'intonation injuste » du tempérament. Aujourd'hui l'une et l'autre méthode sont mêlées (mais pas encore pour tous).

]

...

 

Généraliser la linéarité de la mesure : afin de se repérer dans l'identifiable

 

^y√x ou x^1/y : l'outil de la généralisation linéaire des échelles ?

^y√x ou x^1/y est un nombre irrationnel et réel élément de l'ensemble des nombres réels R qui ne peut pas être représenté par une fraction x/y élément de l'ensemble des nombres rationnels Q. La trace la plus ancienne découverte de l'usage de l'opération racine : élévation à la puissance d'une fraction, date des anciens Babyloniens vers 1700 avant J.-C. visible ici. [√ est le signe élargi de r]

Comment en presque 4 000 ans d'histoire des mathématiques, l'opération racine ne se généralise que pendant la seconde moitié du XXe siècle aux échelles musicales équidistantes ? L'utilisation des fractions pour définir des intervalles (rapports et constantes pour la formation des échelles) n'offre qu'une approximation bien connue des mathématiciens. ^y√x simplifie et généralise la constitution d'échelles avec le nombre de coupures égales dans un ambitus donné.

La simplicité de ^y√x permet de construire un champ de fréquences de fréquences (échelles) vibrantes dans lequel on peut se localiser et réaliser des opérations de métamorphoses entres elles. Puis de former des modes à partir de ses échelles et de les multiplier en gammes.

...

 

 

Notes
[1] La division en 2 de 2 pour obtenir le rapport du milieu par √2 ou ou x^1/2 dans une octave correspond à l’intervalle de 3 tons (6 ½ tons) plus connu sous le nom de triton ou de quarte augmentée (4te+) ou quinte diminuée (5te-) ou « diabolus in musica » dont l’usage était prohibé au XIVe et XVe siècle par l’Eglise catholique. Cette division « dans le milieu » se retrouve à chaque division paire de l’intervalle d'octave = 1,4142135623730950488016887242097...

_

- Afin d'écouter nos exploration d'échelles, nous utilisons le programme multiplateforme Scala dont ses fichiers prennent le suffixe : .scl. Avec le « relaying » de Scala chacun peut jouer et écouter en temps réel (avec un clavier et une interface MIDI) les échelles téléchargées. Scala est un freeware téléchargeable à http://www.huygens-fokker.org/scala. Ce programme en outre exporte les échelles, modes et gammes vers un très grand nombre d'instruments de musique électronique. Nous mettons aussi à disposition les tuning script pour celles et ceux qui possèdent le sampler Kontakt 2 de chez Native Instruments. -

_

Nous nous posons des limites arbitraires du Champ Scalaire pour les intervalles constituants les échelles nonoctaviantes à :

. entre 12,5 cents & 240 cents
. entre Z96 & Z5
. entre 1/16e de ton & 6/5e de ton
. entre ⁹⁶√2 & ⁵√2

pour l'instant, bien que rien n'empêche d'aller au-delà

_

.

.

exploration du connu vers l'inconnu

A LA RECHERCHE DES ECHELLES NONOCTAVIANTES CYCLIQUES OU NONCYCLIQUES

 

 

Quelle est la particularité des échelles nonoctaviantes ?

La sensation de la non-finité de la musique : il n'y a pas d'octave qui donne le sentiment de stopper sa progression ?

La désoctaviation des échelles nonoctaviante rend inutile le rôle de la note sensible qui oblige à une résolution dans le ton de l'octave. Dans le système tonal voire sériel de la division équidistante de l'octave, les transpositions des modes, des séries (donnant les différentes gammes du mode) sur l'échelle octaviante « tournent » sur elles-mêmes : dans le modulo à l'intérieur de l'octave qui est le principe de la combinatoire, même si les intervalles sont doublés ou triplés sur deux ou trois octaves, voire plus. Ils reviennent toujours sur la position initiale du ton qu'oblige la sensible. C'est le principe du tempérament cyclique où chaque identité se retrouve à différents étages de la transposition puis à la cadence, dans la résolution harmonique de l'octave de la tonalité (du ton de la fondamentale). Sans que la forme du mode change. Dans le système non-octaviant, il n'y a pas de sensation de retour à la case départ et les formes des modes peuvent changer dans leurs transpositions. Rien n'oblige à revenir à son point de départ pour terminer sa révolution musicale. L'attraction de l'octave « trou noir » est absente du système non-octaviant et permet des évolutions multiples. Du possible supplémentaire.

 

À la suite des précurseurs explorateurs des microtonalités (Juan Carillo, Aloïs Haba, Ivan Wyschnegradsky suivit par Jean-Etienne Marie), nous poursuivons, approfondissons et relions l'exploration de nouvelles échelles à partir de la division du ton qui sera suivi par la division de l'octave (Harry Partch) pour nous enfoncer plus loin dans la découverte d'échelles non-octaviantes [1] asymétriques ou ayant des propriétés jusque-là inconnues pour former une « carte » d'un réseau de liaisons (scalar-system-field) qui permettra de « voyager dans ces contrés encore inconnues » (autres musiques).

Je ne saurais dire pourquoi l'exploration des micro-intervalles en Europe a débuté avec la division du ton. Toutes les déclinaisons de micro-intervalles sont nommées par les fractions du ton. Avec Harry Partch sur la côte ouest des États-Unis et à partir du livre d'Hermann Helmholtz (On the Sensation of Tone)*, il décline ses micro-intervalles à partir de rapports (fractions) de la division des cordes. Le système des micro-intervalles d'Harry Partch est harmonique** contrairement au système des Européens Aloïs Haba et Ivan Wyschnegradsky qui est tempéré (bien qu'Ivan Wyschnegradsky tend à concilier les deux). Le système (antérieur aux deux autres) du mexicain Juan Carillo se situerait entre les deux, quoi qu'il nomme ses divisions d'échelles par des fractions du ton.

Notes
[1] ne pas confondre, mais issu à la suite des « espaces non-octaviants » (vers 1932) d'Ivan Wyschnegradsky (1893 - 1979) : « Un espace non-octaviant est un espace dans lequel l'intervalle de l'octave, qui depuis les temps les plus reculés avait délimité la périodicité de l'espace, se trouve soit contracté soit dilaté d’une ou plusieurs unités spatiales, de sorte que la fonction qui traditionnellement incombait à l'octave naturelle, est reportée sur des octaves modifiées*** » Ivan Wyschnegradsky cité par Franck Jedrzejewski dans son Dictionnaire des musiques microtonales. L'idée d'échelles sans octave n'est pas nouvelle. Dans la technique d'écriture sérielle les compositeurs (Messian, Boulez, Riotte, etc.) utilisaient l'opération de modulo (cycle) pour retirer à l'octave sa primeur : au lieu d'un modulo 12 ils posaient d'autres modulo, mais toujours dans le champ de Z12 : « éviter l'octave c'est se libérer de la domination de la tonalité » qui reste sous-jacente en utilisant l'échelle Z12 ou autres divisions de l'octave. Ici avec le terme « échelle non-octaviante » nous ignorons, évitons volontairement l'ambitus d'octave « trou noir » et fouillons dans des asymétries subtiles (« Une des conséquences immédiates de la révolution ultrachromatique est l'incorporation au langage musical des sons harmoniques supérieurs inconnus dans le système tempéré des 12 demi-tons. » Ivan Wyschnegradsky, La Revue Musicale 290-91) pour élargir le champ des possibles (nous avons définitivement quitté Z12) à la découverte de ce que nous ne connaissons pas : d'autres sonorités d'échelles aux propriétés transitionnelles : pour des glissements progressifs de sonorités à d'autres : une toile élastique d'échelles en mouvements.
* La traduction « poétique » de Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik (Sur la sensation de ton comme base physiologique pour la théorie musicale) titre qui ne sonne pas en français ? fut publiée sous le titre Théorie physiologique de la musique, ne lui laissa aucune chance d'attirer l'intérêt des acousticiens ni des compositeurs. La traduction anglaise donna à Harry Partch l'outil nécessaire pour construire ses échelles originales.
** L'intonation juste (just intonation) lui est pérennisée [téléchargez ses 13 échelles au format .scl] puisque des compositeurs de la génération suivante tels que La Monte Young et Ben Jonhston (qui fut son élève) ont continué la division entière des rapports de fréquences du système harmonique pythagoricien transmit par Hermann Helmholtz. Ben Jonhston l'adapta à son écriture sérielle (décrit dans son article : Rational Structure in Music en 76) et La Monte Young à son écriture minimaliste de « drone » (bourdon). Cette adhésion à l'intonation juste des compositeurs américains s’est inscrite en réaction aux compositeurs européens utilisant le « tempérament juste ». Aujourd'hui le mouvement élargi est rassemblé sur le réseau Internet sous l'appellation : The Just Intonation Network à http://www.justintonation.net (fermé fin 2011 puis réouvert en 2012). L'intonation juste est définie comme telle : un système d'accordage dans lequel les intervalles sont représentés par des rapports de nombres entiers. L’« intonation juste » utilise l'opération division simple [/] et le « système tempéré » l'opération racine [√] : une division en puissance. Aujourd'hui cette position n'a plus vraiment de sens puisque personne à l'oreille n'attache d'importance à déterminer si un intervalle fait partie du camp de l'intonation juste ou du camp du tempérament juste : les camps aujourd'hui se sont mélangés pour découvrir autre chose où il suffit de s'accorder. Bien que certains s'y accrochent : une croyance même fausse est difficile a lâcher.

*** Pour nous,
l'octave dans nos échelles nonoctaviantes n'est pas modifié,
puisqu'il ne représente pas le cycle de l'ambitus divisé.
Ce n'est pas l'octave modifié qui répète le cycle, mais un autre intervalle.

Les échelles nonoctaves de Shadow-Sky commencent leur révolution en 1982.

.

Manuel Op de Coul (Scala program maker) asks Mathius Shadow-Sky a question in June 2012:

Manuel Op de Coul : By the way why are all your scales based upon multiples of 100 cents?

Mathius Shadow-Sky : Thank you for asking: this is a Very good question! To be more exact it is more 200 cents than 100 cents: the tone than the half-tone. I started from what we know (of what I know), by continuing the 'tradition' of European scales exploration made by: Claude Debussy, Ivan Wyschnegradsky + Alois Habba, Juan Carillo (Mexican), in relation with Jean-Etienne Marie, and formalizators like Pierre Barbaud, Iannis Xenakis, and André Riotte. This is the first step, to not loose the reference point of what we know, and going in what we do not know. The nonoctave scales multiple of 200 cents show that nonoctave scales exist also in extended tonal scales ensemble. I think that the process of recognition of what we do not know, is easier starting with what we know. As an understandable mark of what we do not know. The second step will be: to go further, out of tone multiple scales especially with prime numbers. Without any marks, it would be impossible to build the 'Scalar-System-Fields', because equal tempered scales work as marks in the nonoctave scalar matrix system (a sort of multidimensional elastic material of nonoctave tempered scales), and to build up from them (with several nonoctave equal tempered scales): modes (scales with at least two different interval from two different tempered scales). This is the starting point to generate a mapping of unknown tunings and chords as an extended harmony out of tonal harmony of 100 cents and its 'black hole': the octave, and also to integrate all other scales in an understandable communication system. Also by your question, it is possible I miss something I should not. What do you have in mind? I was thinking about the 3000 scales you propose with Scala, does it needs a certain information about how each one was generated? And perhaps also a system to understand them in one shot, than to try them one by one? It is really what I am trying to do with my nonoctave scales. It is just the beginning, the work seems to be huge!

.

A la recherche des échelles nonoctaviantes dans la division du ton

A la recherche des échelles nonoctaviantes dans la division de l'octave

A la recherche des échelles nonoctaviantes dans la division des nonoctaves éléments de Z12

A la recherche des échelles nonoctaviantes à partir des intervalles de la série harmonique

hauteur
intervalle
échelle
mode

suite

re tour à la table des matières